

�ƥ�����ʬ�Ϥ˥����ѥ�����ؤ伫������������θ����쥳���Ƴ�����Ƥɡ��Τ����Ρ��Ȥ����Τ���Τ�ꤿ�����ȤʤΤǤ����������ͽ�۳��˷㤷�����åѥꤷ���˹礦�Ȥ����и��Ƥ��ޤ������ǡ����Ρ������ϡסʡ��ˤ�̵�뤷���ͤ��ʤ���Ϥ�����������碌�Ƥ��ʤ����ᡢ�����������¾̤��ƺ��˻�롢�ȡ�
����Ǥ⺬�������ܤʤΤǡʢ����˰�����θ���ʬ��ʬ�ʤ�˺ƹ������Ĥ�ʬ�Ϥ����Ŷ�����õ�ä��ꡢ������¹Ԥ��ƿ������̤Υ��쥳��ߤ����ʤ��ȤˤĤ��Ƥ�Ƴؽ��ʡ��ˤΤ褦�ʤ��ȤƤ��ޤ�������������Ȥ�����ȤǤ�����������ʤ�˻�������ä������⤢��ޤ���
��˺ϿŪ�ˤ����������Ȥɤ���˽Ȥ�褦�Ȥϻפ��Ĥġ��褯���ΤäƤ���ʬ��ǤϤʤ��Τ�ʬ���ä��Ĥ��Dz������㤤�Ƥ���Τ��⤷��ʤ��¤�����դ�Ż�������������ܤʤ���ʢ������ˤ��γ�ǧ��Ȥ��Ѥ�ޤ�...�Ȥ������������Ƥ��뤦���˴�������
������˺���Ϥι�ǯ��������Ǥ⤢�ꡢ���Ǥⲿ�Ǥ�Ȥˤ����Ĥ��Ƥ����������ɤ���������Τ����Ѥ��δ����ǤȤꤢ�������ܤ�����Ƥ����ޤ��롣
����dy/dx�פ�ʬ�����ݤ�����
�������礬����ʬ�ˤĤ���
������������ˤ��֥����֥顼�κ����ײ���
���¤�����������˳������㼨
���������ȥޥ륳��Ϣ��
�������UFO�����
���ݤ��������Ū�˼�����ˡ
�����ϡָ�������Τ�ʸˡ�Ǥ��ꡢʸˡ�������Ǥ��뤫�顢����������Ǥ���פȤ����ͤ������н褷�褦�Ȥ����ٶ��ʡ��ˤ��Ƥ�����Ǵؿ�����ä��ꤷ�ƹͻ��������ȤǤ��ʢ���Ȥ����Ǥ�ʤ��Τ�ޤޤ�Ƥ뵤��...�����������ؤ������ȼ�������δ֤ˤ��륢�쥳��˴ؤ��뤳�ȡ��Ȥ�����뤫�⤷��ޤ���
�����������Ƥ���ֳݤ����ν�����궯������פʤκ���ˤ�ָ�����ܼ��������Ǥ�����ؤ��ܼ�������������ξ�Ԥˤ��б��ط�����Ω���Ƥ�������Ѵ����ǽ�Ǥʤ���Фʤ�ʤ��פȤ�����ǰ�����ꤽ���Ǥ����ޤ����ο�ǰ����ϡ���������ؤ�����Ʊ�ͤ�����Ū�ʤ�ΤǼ�Ѥ�ƨ�줿�Ҵ�Ū�����ʤɤ�¸�ߤ����ʤ��פ���ӡָ������������ؤ�Ʊ�ͤ˵Ҵ�Ū�����˴�Ť������ʳؤ��оݤǤ���פȤ�����ȿ�����ĥ�������Ƥ���Τ��¬�Ǥ��ޤ��ʢ���Ԥ�Ω��ʡ�����ʸˡ�ɡˤ��鸫�����ԡʡ�����������ˤؤμ�ٹ�ʹ���ˤĤ��ư��������Ȥ�����ޤ�...����������ξ�ԤΤ����ɤ��餬�������Τ������䤦���Ȥ˰�̣������Ȥ�פ��ޤ����θ��ݡʡ��ˤ�ñ�ˡָ������������ؤϻ��Ƥ��ʤ��פȤ�������ץ�ʻ��¤����Ƥ�������ǤϤʤ��Ǥ��礦����
���ؤ���ˤǤϡ����ؤǰ�����ǰ�����μ�ˡ���Τ�Τ�ȯŸ���¤�ǡ�ɽ��ˡ�β�������ߤ��Ƥ����褦�Ǥ����ǽ�ϼ��������ʤȺ�ޡ�����ɽ���˻Ȥ�����ʤ��ʤ��ʢ�����ʸ�����ˤ���ȥԥ����ʤ��ΤǤ������奮�ꥷ���ǤϿ�����ɽ�����Ѥε��椵��¸�ߤ�������ե��٥åȤ����Ѥ��������⤽�γ�����ƤϺǽ��9ʸ����1����9����9ʸ����10,20,30,�Ȥ���������90�ޤǤȤ��Ȥ����Ψ�ζˤ�...���������Τ�����ؤǰ�����ǰ���������켫�ȤȤ��̤ε��楷���ƥ�ʤǤ������ʤɡˤαƶ��������ƻͤ�����������������ä����Ĥޤ꼫������αƶ����餤���ˤ���Υæ���뤫���Ȥ����ΤϿ��ؤ�ȯŸ�ˤ����ƽ��פʼ���Ȥߤ��ä��ȸ��ä��ɤ��Ǥ��礦��
Ʊ�ͤΤ��Ȥ������ˤ�����ơ����ؤdz�ȯ���줿��Τ�Ƴ��������Ǽ�������ˤ�����¤����ʿ��ؤ�16�����������ؤ�19�������餤���ˡ�æ���ޤ������ǡ����θ�Ͽ��ؤȰ��β��ʡ��ˤ��ĤĤ���ޤǤ����ڤ����Τ褦�˲�ä���ƹ��ٲ����Ƥ��ä��ΤǤ����顢�����˼������줬���ƶ���Ϳ���Ƥ��������狼��ޤ�������ˤ��Ƥ⥢�ꥹ�ȥƥ쥹�λ���ȥ֡���䥫��ȡ���ޤǤδ֤˹Ԥ���2000ǯ�ʾ�ˤ錄��ġ����Ѥ߾夲���Ƥ�������ʸ���ˤ��ʽ�衩�˵���������Ū���������鸫����...�Ȥ������ȤǤ����������ۤ�������̣���ʤ��ä����Ȥ����Τ��ڤʤ���ʸ���ˤ���ۻ�Ū�ˤ�ͭ�յ��ʻ����ˤʤ��Ǥ��礦���ɡ�
�ʲ�����Ǽ��������ܤˤĤ��ƴ�ñ�˥����Ȥ��Ƥ����ޤ���
��������ض���dzؽ��Ԥ������¥�ʤ���ɤ��������𤵤��븶���ˤʤäƤ���褦�ʶ�������¿�����롢�Ȥ����褦���ä���ָ��ޤ������Τ�������ʬ�˴ؤ����Τǡ�dy/dx�פ�ʬ����ª���ƤϤʤ餺���ɤ�����֥ǥ������å����֤�Υǥ����磻�פǤϤʤ��֥ǥ����磻�ǥ������å����פȤ��ʤ���Фʤ�ʤ����Ȥ����Τ�����Τ��Ȥ���
���⤽��dy/dx�������ä��Τ�����פ��Ф��Ƥߤ���ʢ��ʤˤ�����إץ饹����Ӥä��ȳ�ʬ���餤��������⤬�ʤ�ʸ�Ϥ����Ǿ�ǽƤ���Τǡ��ޤ�������ޤ���...�����֤�ؿ�y=f(x)�Ρ���ʬ������differential coefficient�ˡפ����ǤȤ��뽸��Ǥ����ѿ��Ǥ���������������ȡ���Ω�ѿ�x���Ѳ��̤ȡ�������б�������°�ѿ�y���Ѳ��̤���ζ˸��͡פȤ������Ȥ��ȡ�
��Ȥδؿ�y=f(x)����Ω�ѿ�x��ή�ѡʡ��ˤ��Ĥġ�dy/dx����Ф��뽾°�ѿ��Ȥ��뿷���ʴؿ����Ȥδؿ����Ф����Ƴ�ؿ���derived function�ˡפȸƤӤޤ������Ȥ��ƽ�dy/dx=g(x)�Ȥ������ȤǤ������̤�dy/dx=f'(x)�Ȥ����褦�˽��ʢ���dy/dx�פϥ饤�ץ˥å������ǥץ饤����դ���Τϥ饰���ή�餷���ä�...�����路�Ǥ����ǡ��ؿ�y=f(x)��Ƴ�ؿ�y'=f'(x)����뤳�Ȥ�ִؿ�y=f(x)��x�ˤĤ�����ʬ����פȤ���������
�ä����ɤ��ʤ�ΤǦ�-����ˡ�ȥ��ߥ��ߤǰʲ��ˡ����ؤϸ����١ʿ��浪�ҡ�2009�ˤθ����ʡ��˵��ǥڡ�����p.141�ˤ�Ž�äƤ����ޤ��Τǡ�����ʴ����Ȥ������Ȥǡʢ����ˡ�
���ơ��ä��ᤷ�ޤ���
>> dy/dx��ʬ�����ȸ��ʤ��ʤ��Τϥȥ�ǥ�Ǥ�̵��������togetter��
bit.ly/2h7ksMT �������������֤��ʤ��Τǡ�������ˤ�����Ȥ����������ȻפäƤ���Τ����ɡ���\int(x/\sqrt{x^2+4})dx=(1/2)\int(1/\sqrt{x^2+4}))dx^2+4=sqrt(x^2+4)�Ȥ������Ƥ��ФƤ��ƥӥå��ꤷ����dx^2+4�Ϥ����d(x^2+4)�ȽƤۤ������ɡ�������ƨ���дְ�äƤʤ��Τ������Ȥ������Ȥˡ���16 Dec 2016��
togetter�ޤȤ����Ƭ�˽ФƤ���tweet������ѡ��դ��Ĥ�ȯ����Ҥ��Ƥ��ޤ����ʤ��ǽ�˽ФƤ����ϡ�dy/dx��ʬ���ʤΤ��ݤ���dxʬ��dy���ɤ�Ǥ����Τ��ɤ���������ʬ��ɤ�������٤������ɤ�ǧ�����٤������פȤ���togetter�ޤȤ�ؤΤ�ΤǤ���
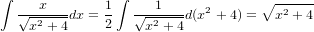
ȯ����ο�����ʬ���狼��ˤ����ΤǤ���äݤ�ɽ���ˤ��Ƥߤޤ�����������ʡ��ˤνФƤ�����ʬ��ȿ�Ǥ����Ƥ���ޤ���������ü�μ�����ɤ����ƿ�����μ��ˤʤ�Τ��狼��ʤ��������줬�ɤ���äƱ�ü�η�̤˷Ҥ���Τ�����Ǥ��ʤ��ΤǤ������Τ��ˤ������dy/dx��ʬ�����ɤ����ߤ������ä�̵�ط��˲Ƥޤ��͡�
���ʤߤ˲������Τ��դ�ʸ��Ǿ�Dzʡ��ˤʤ�dx��dt��ɽ������������Τ�ʬ���äݤ�������ʬ�����äƤ��ޤ������ζ���Ū���쥳���ʲ��˽Ф��Ƥߤ뤳�Ȥˤ��ޤ��礦�ʤʤ���äݤ��Ǥ������С������Τ����ִ���ʬ�פȤ�������ˡ�Ǥ���
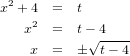
�嵭�η�̤�t����ʬ���ޤ�����ñ�Τ��ᱦ�դ����ξ��������ޤ�����Ǥ�ǽ�Ū�ʷ�̤�Ʊ���Ǥ���
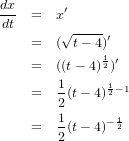
����ʬ��...�äݤ�dt�ʢ�dx/dt��ʬ������ʤ��Ȥ����ʬ��ȤϤ����ޤ�����͡��������դ˰ܹह���dx��t��dt��ɽ���ޤ�����
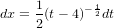
�����ޤǤη�̤�Ȥäƺǽ�μ��Τ褦���������ޤ���dx����ʬ����α�¦�˽줿���˳ݤ��Ƥ���ҤȤĤ��ѿ��Τ褦�˰��äƷ����Ƥ��ޤ�������ʬ�����dx�ϳ�̤Τ褦�ʤ�Τ���ĥ��åȤǤҤȤĤε���פȤ�����dy/dx��ʬ���ǤϤʤ��������Τ��Բ�ʬ�ʤҤȤĤε�������Ȥ����Τ�Ʊ��ξ��̤Ǥʤ������������Ȥ�����������褦��...��
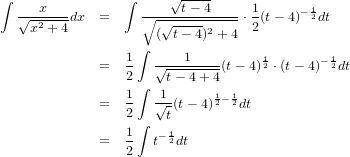
�������ʬ���ޤ��ʢ���ʬ�������μ��ˤ���t����dt��t��ʬ����̤���x^2+4���ִ������tweet�ˤ��ä����ο�����Υ�Ĥˤʤ�ޤ�...�Ĥޤꤳ�����٤η���Ǿ������ǺѤ�Ǥ��ޤ��櫓��...������ñ�Τ�����ʬ����Ͼ�ά���ޤ�����
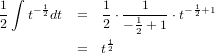
���t��xɽ�����ᤷ����������Ȱ��Ѥ���tweet�ˤ��ä������Ȱ��פ��ޤ���
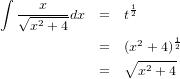
�ǡ����η�ˤĤ��Ƥɤ��ͤ��뤫���ʤΤǤ������ޤ�������Ū�ʤ��ȤˤĤ��ƿ��ؼԤε����˸���ʤɤȤ������ȤϤ������ޤ����Τ���������Ǥ������ۤ϶�Ū�ʡ�����Ǥ�ҤȤĻ�Ŧ���Ƥ����������ʡ��Ȼפ���Τϡ���������ʡ��ˤ����������Сֿ��ءʤ�ʪ���ˡפߤ����ʹ��ޤˤʤäƤ������Ǥ����ʤ��Ѥʸ������Ǥ�����
�����ȡ��Ȥ��ɤ����Ѥ��Ƥ���������λ���������ɴ���١ʿ��ض��鶨�IJ�,2005�ˤο��ؼԾ��������ʡ��ʡ��ˤ˾�ʿˮɧ�Ȥ������ܿͤǽ��ƥե����륺�ޤ���ޤ����������Τ��Ȥ��ܤäƤ���ΤǤ����������˵��ˤʤ뤳�Ȥ��Ƥ���ޤ�����
��ǯ�����ܤ���ꡢ�����ض������ؽ�����ض�������Ǥ�����س��ν��äȤ��ƿ��ض���ؤ�ȯ�����Ѷ�Ū�˹Ԥ������ض��鸽�岽���Ȥ�櫓�������ο��ض���ؤ�Ƴ���˶�������ȽŪ���ؤ�ĥ��ޤ�������p.399��
�������˽��������Ƥɤ��ʤ�Ȥ����Τ����Ȥ����ä餷���Ǥ������֤�1971ǯ�˼»ܤ��줿�ؽ���Ƴ�����ʢ���äȤ�ͤ���ߤ��ä���ġ��Ǥ����ʤäƤ����Ȥ���Ƚ�����ΤǤ��礦���������Τˤϡָ��岽���ꥭ����פȤ���¯�Τ�����餷���Τǡֶ�������ȽŪ���ؤ�ĥ�פä��оݤǤ���ֿ��ض��鸽�岽�פȤ����Τϡָ��岽���ꥭ����Ǥο��ض���פȤ�����̣���ȡ�
>> �ָ��岽���ꥭ����פȡ֤�Ȥ��������ĽΡ�
�㤨�а�����Ϲ�ˤޤDZ���졢������ؤǶ����Ϥ�Ƥ��뻻�������ؤΡֽ���פ������Ͼ��ع��ǽ��äƤ��ޤ��������ǯ�ǽ��ä�������Ρֿ��ح��פ����Ƥˤϡ����ι������ǯ�ʾ�ǽ������Ƥ������˵��ܤ���Ƥ��ޤ����ʻؿ��ؿ����п��ؿ��ʤɡˡ�����ؤϡ֭��פǻ��¾�ؤ��ϰϤ�Ⱦʬ���餤�ޤǥ��С����Ƥ����ΤǤ������ܤ�ȯŸ�Τ���˶���Ͻ��פ������Τ���ˤϲ��Ƥ��¤ֿͺ�������Ǥ���ָ��岽�פ��ʤ���Фʤ�ʤ��Ȥ���������ä��ΤǤ���
�����ϰ��ѼԤ��Ĥ��ޤ����������ǡֿ�����פȸ����Ƥ���Τ��ָ��岽���ꥭ����פǶ�������������Τ��ȤǤ����������ˤ���褦�˾��ع��ǽ��������äƤ���Ǥ��͡��ޤ��ֽ��������ä��פȸ��äƤ����ƤϿ����ʤ���Ȼפ���Ǥ����ʢ��Ƥ����������Ƚ���ϥ��åȤǶ����ʤ���������̣�ʤ����龮������ˤ�̵�������ݤ��������ʤߤˡ־�ʿˮɧ�סֽ������פǥ����ä���ʲ��θ�����𤬥ҥåȤ��ޤ�����
>> �����ض���ϤɤΤ褦�ʽ���ǹԤ��٤����סʼ��м�,1977��
������ǰ��Ѥ���Ƥ���Τϡ����ض�����Ĥ���� (��嶵��Ϥ���Ǥ����Τ�)�סʾ�ʿˮɧ,1975�ˤǤ���
�ֿ��ؤζ���ϡ����ؤ����ŪȯŸ�ν���˽��äƹԤ��٤��Ǥ��롣��ʪ�θ��Τ�ȯ���Ϥ��η�����ȯ�����֤��������ؤζ���⤽���Ʊ�ͤǡ�����Ū�˴���Ū�ʳ�ǰ�������Ū������줿��ǰ�ۤɻҶ��ˤȤäƤ狼��פ������ν����դˤ��ƻҶ��˶����褦�Ȥ���С�����ʬ����ܼ�Ū����ʬ������Ǥ��ʤ��Τǡ���ɡ����ܼ�Ū�ʤĤޤ�ʤ���ʬ���뤳�Ȥˤʤ�סֹ����ع��ޤǤ˶���������ؤ�18������ȯŸ��������ʬ�ޤǤǤ��������������ä�19�������ˤϤ��ޤä��������ع��Ƕ�����ʤɤȤ�Ǥ�ʤ��ְ㤤�Ǥ���ס־������ˤ��г�����ˡ��¿���狼��ʤ����顢�������κǤ�Ĥޤ�ʤ����ɤ��Ǥ�褤��ʬ���뤳�Ȥˤʤ롣�������˶����뽸�����Ϸ褷�����Ϥʤ���������Ͻ������κǤ�Ĥޤ�ʤ���ʬ������Ǥ����
���С�1977�ˤ˰��Ѥ���Ƥ��뾮ʿ��1975�ˤս�ȴ���Ф��Ƥߤޤ������ǽ�Υ�Ĥ�˧��ʡʡ��˥ȥ�ǥ⽭�����Ƥ��ʤ����Ȥ�ʤ��Ǥ��������Ȥ���ĤϤޤ��������ʡ����ʢ��ե����륺�ޤ��������䤾����äȷɰդ���ơ������������ܤΥ�Ĥ˽����н������Ͼ��ع��ɤ�������Ƕ����Ƥ����Ȥ������Ȥˤʤꤽ���Ǥ���
���������кǶ��ʢ������ǯ����ΰա��С���twitter�Ǹ�����������ΤǤ������ɤ�������ؤǿ������Ѽ��Ȥ��������濴�Υ��ꥭ����ˤʤäƤ��뤳�Ȥ���Ƚ���Ƥ��ޤ���������ʤ��ȡʡ��ˤ�äƤ�֤˹���ٶ��������Ȥ�����˺��Ƥ��ޤäƳ����ΤۤȤ�ɤ���ؤǤο��ؤˤĤ��Ƥ����ʤ��ʤä��㤦�ʡ��ˤߤ����ʴ����ǡ�
�������������Ȥۤ�Ʊ���ʢ����դ�ʸ�Ϥ���鸫��...�äƤ��ȤʤΤǥۥ�ȤϿ��������⤢��Τ���...���ʤΤǡ������������Ҥ��ˤ���Ȥ����Τϡ�����ޤdz������Ƥ������ؤǻȤ��뿧���ʳ�ǰ������Ū�����Τʤ�Τ������ľ����������ʡ��ˤȻפ��ޤ��롣����Ͽ���ǽ�Ϥ�������ɬ�פʤ�Ǥ��礦���ɡ���ǰ�ʤ��餽�β��������Ǥʳ������Ѥ��ڤ줺���٤�Ƥ��ޤ����ȡ��ǡ��Ƽ���ɬ�פ˱����Ƥ���ʤ��ƻ��Ȥ��ƻȤ���Ф��������ʤΤˡ��ʤ�Ǥ���ʤ��Ȥ���Ρ������䡪�Ȥ�����ĥ���ä��Τ��ʤ�...��
��ͤοʹ֤�������ǧ������Ȥ����ǽ餫�鸷̩����̩�˰���Ū�˸�����櫓�ǤϤʤ�����������Τ�������������¤��ط����狼�ä����ΤǤ��롣����ά���㤨������ʬ�����硢�Ϥ��ᤫ��¿���Ϣ³�����-����ˡ���Ƥ�����ʬ���ܼ��Ϗ�ۤ������Ϥ��ޤä�����������ʬ�������Ǥ��ä��褦�ˡ�;�긷̩�ʻ��Ϥ��鷺�ˡ���ʬ���Ѥˤ�ä����Ѥ������ʿ��®�٤ζ˸¤Ȥ���®�٤���ꤷ�ơ��������ޤ줿�����λѤ�̣�碌��������帷̩�����̲����줿��Τ���٤��Ǥ�������������̩������̲�����ؤν��פʻŻ��Ǥ�����˰㤤�ʤ��ΤǤ��롣
�嵭�Τ褦���ʢ����������ϰ��ѼԤ��Ĥ��ޤ������������С�1977�ˤǤ϶������Ф��ƾ�ʿ��1975�ˤΡ����ŪȯŸ�ν���פǿ��ض���٤��Ȥ�����ĥ����������ǧ��ޤ��������ºݤ˿��س�ʬ��Ρ����Ū�ʰ��֤Ť����פ��ꤹ��Τ�����͡��Ȥ����̤������ꤷ�Ƥ������������äȸ��������ʤΤǤ褯�狼�äƤޤ��ɡ�
�Ȥ����Ǻǽ�β������ʤ�Ǥ����ּ¿���Ϣ³���פ�����ʬ������˶����Ȥ����ߤ����ä��ʤ�...�ȸĿ�Ū�ˤϻפ�ʤ��⤢��ޤ������äƤ�Ȥ����Ȥ߹�����͡�Ū�ʡ��Ȥ��������ѿ��׳�ǰ�������»�ʤäƤ����ʢ������⼫�Ф�̵���ä�...����á��������Ǵ�Ϣʬ�������ʢ��ۤܿ��������Ȥ����...���ޡ��������å������Ƕ�ϫ�����ȤȤ��Ƥϡ�Υ����Ϣ³�פϺǽ��׳�ǰ����ʢ��ޡ����������ΤϸĿͺ������뤫��ï�ˤȤäƤ��ɤ����֤ʤ�Ʒ����̵���äݤ�...����Ϥ狼�뤱�ɤ�...���ȼ�ĥ������������Ϥ�ä�ۣ��ʡֿ����̡�ʬ�Ȥ������DZѸ�Ǥ�ɬ�פˤʤ뤷��
���⤽����س��ʡ��ˤˤ���������ʬ�Ȥ����Τϴؿ���������Ĵ�٤�ġ���Ǥ��ä��ʢ������⼫�Ȥ�ؿ���������ʬ����ʬ�Ȥ�����KUFU���������������ΥΥ��ϥ���ʬ�Ϸ�̤ν��Ѥ����ϳؤʤ櫓����ʢ��Ǥ���͡����ʤ�Ǥ���������ȯ�ǻ볦�ꥢ�ˤ�����¡ʡ��ˤ��Ƹ���ʤ��櫓�������ᡩ�櫓�狼���衣�Ƥ������ع����餳�ä������äȲ��餫�ο���Ū�о��ʢ����Ȥ��������Ȥ���§�黻�Ȥ�����������Ĵ�٤���ˡ�Ȥ������Ū���̤�ؤ�Ǥ��Ƥ����櫓����������ʬ�⤽�α�Ĺ��ˤ���...���ä����ɥ���������Х�����...�ȹͤ���Ф������������������祤�����Ƥʤ��ȱ䡹��ٹ�˿����ʴؿ�������ʬ������ˡ�ˤĤ��Ƴؤ�Ǥ�����Ԥΰ�̣��狼������������ִؿ��Ȥϡ��פߤ����ʺ��ܤ���ۣ����ä����ʡ����ض��鳦�Ϥʤˤ�äȤä���䡪�ʢ����οͤ�ˤ�����𤬤���ͤ��...���ʤäȤ��Ǥ�����
�����ȡ��ä����ä��㤳�ä��㤤�äƤޤ��Τ��ᤷ�ޤ�������ܤβ������ˤ���ֶ�ʬ���ѡ�ˡ�������Ǥ褯�Ȥ����sum�פΡ�s�פ����������������ε����������ʢ����ϥ��ꥷ��ʸ����s�ˤ�������������s��Ĥ˿��Ф������...�餷��������ʬ�������ǥ��å����������ȻפäƤ��ΤǤ������ʤ������ḷ̩������Ω���ʢ���ǾҲ𤷤�togetter�ޤȤ�˽ФƤ��뽸�������������ĥ������Ϥ�������ꤵ���餷���Ʒ빽����å���
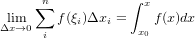
����ϡ����ؤ�̵�¤��Ϥ��١ʥ�С�,2013�ˤ˺ܤäƤ�����Ρ�¾�ˤ��㤨�Х����äƤߤĤ�������ʬ����ˡ�δ��ܼ��פ˰ʲ��μ�������ޤ���
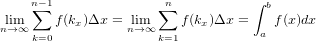
�����襵���Ȥˤ��뼰�Τޤ̤�����Ǥ������ʤ��ѤǤ����...Ѩ�ۤʤ�������ʡ��ˤ�Ƚ�Ǥ��ưʲ��˽����Ǥ�
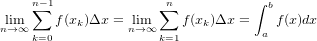
�ǡ���С���2013�ˤ�Midpoint�Ǥ�äƤޤ������ä��μ���Upper Sum��Lower Sum��ռ�������Τʤ�Ǥ��礦�����ʢ����䤫���ˡ�����餬���פ��Ƥ���ȡ֥�ޥ����ʬ�פȤ�������Ǥ����ä����ʢ�������������ʸ�Ϥ���������...���硼���ʥ��͡�
�Ȥ����Τ褦�˻פ���Ⱥ���ΤǤ��� ����ʬ�ϡ�������ʬ�䤷�����夲����̡ۤǤϤʤ�������ľ�����ޥ��¤ζ˸¤Ȥ�������ɽ��������Τȹͤ��ޤ������κ��Ͻ�ؼ����Ǥ⡢�����٤�ʸ̮�Ǥ�̵��Ǥ��Ƥ⡢�����٤����Ȼפ��ޤ�����30 Dec 2016��
togetter�ޤȤ�ν�������������ȯ���Ͼ嵭�Τ褦�ʴ��������Ѥ˺ݤ��Ƹ�����ؤΥ�ϳ䰦���Ƥ��ޤ����֥�ޥ��¡פˤĤ��Ƥϰʲ������ͤˤʤ뤫�⡣
>> Riemann Sum��WolframMathWorld��
��˺ϿŪ�˴�ñ�˥����Ȥ��Ƥ��������ΤĤ�꤬���𤷤��ޤ�Ĺ��ˤʤäƤ��ޤä��Τǡ����ʤ�ͻ��Ȥ����Ȥ����ޤȤ�ߤ����ʤΤ�̤��������ƥ֥��ڤ�ˤ��Ȥ��ޤ�������ޤ������ȡ�����Ǥ����ͤˤޤȤ�ո�Ū�ʤ�ΤϻĤ��Ƥ����ޤ��礦��
dy/dx������ʬ�ˤĤ��ơʤ����ǤϤʤ��������̤ˤ����ơ˶�����äȤ���θ���ʤ��ƤϤʤ�ʤ��Τϳ�ǰ�γ����˹�����褦�ʼ�������ʤʤɡˤǤ��������ɤ�����٤����Ǥ��äơ���������ʤʤɡˤǤ�äȤ����Τˤ��γ�ǰ��ɽ������ʡ��������ˤˤϤɤ�������ɤ������ǤϤʤ��������ɤΤ褦����������г�ǰ���������䤹���ʤ�Τ��ϳؽ��Ԥˤ��Ŀͺ����ʤ��֤��ʤ�ˤ��äư쳵�ˤϸ����ʤ���
��ʬ�˴ؤ��Ƥ�����
��dy/dx�ϤҤȤޤȤޤ�ε���ע���ʬ�������Ȥ��ѥ˥��ä�
�֢��dx�ǤҤȤޤȤޤ�ε���ע���ʬ��ǰ�����˼��Ԥ���
�ּ¿���Ϣ³�����ʤ��ע���Ҥ����̤�
�֦�-����ˡ�ע������Ƥⶵ���ʤ��Ƥ�ɤä��Ǥ⤤��
����ʬ��������ʬ�䤷�����夲����̤ǤϤʤ��ע����֤��𤹤�
�ߤ����ʴ����Ǥ���
�ؤ�����쥫���٤Ȥ������Ȥ�2005ǯ2��27��������˥����ȤȤ��ƽб餷�������������������ޤ����ʢ�1978ǯ2��28�����ޤ�������ʤΤ���ؤ�´�Ȥ��Ƥ���4ǯ���餤�Ϸв�����������Ƥϥۥ磻�ȥܡ��ɤˡּ�������ʬ���ͤ����פȤ��äƤ��β��˼�����Ƥ���Ȥ�����ΤǤ���
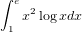
�����ϡ֤���Ϥ⤦�����ʤΤ�...�ѡ��äȤ�ä��㤦��...�פȸ����ʤ�����ʤ��ʲ��Τ褦�˲Ƥ����ޤ����п��������������Ƥ��ޤ������Ǥ����ʢ����ܤι���ض���Ǥδ����˽��������ȵڤӿ��ꤵ������Ԥΰտޤ���ͥ��ԥ���e�Ǥ����Ƚ�Ǥ��Ƥ���褦�Ǥ���
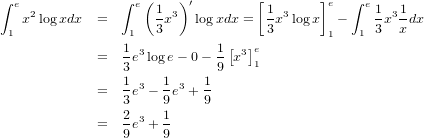
���Τ��Ȼʲ�ԤΡ֤��Τ��餤���ȸ��������Υ��Ƥ�Τ˥��äȤ����������פȤ����䤤�ˡָ����ʤ�Ȥ��Ф��Ƥ�Ф����ޤ��פ������ޤ��������줫��ֿ��ؤ�̥�ϡפˤĤ���ʹ����ưʲ��Τ褦���ä��Ф��ޤ���
���μ��������������Ĥޤ�ʤ���Ǥ��衢���Ρ������طʤ����ä������äơ�����Ϥ⤦���ä�������Ū�ǥ��ꥢ�ǰ������ޤ��̵���Τǡ����줬�狼��ȡ��ʤѥ��뤬���ߤ����ʡ����������ä�����İ�ġ����ä��ꤷ�����������äơ�����Ǥ狼��ȡ��դ˰ŵ�ʪ�Ȥ��ä����аŵ�������Ȥ����ʤ��ȡ��������ƤǤʤ���Ǥ����ɡ�����������������狼��в��ˤ�Ф��Ƥʤ��Ƥ�����顢������������
�����Ǥϡָ�����Ф��Ƥ����ΤDz���Ū�ʤ��Ȥ�����Ĥġ��嵭ȯ���������ˤ���褦�ˡֲ���Ф��Ƥʤ��Ƥ��פȤ��ä��Ƥ��뤿�ᡢ��̷�⤷�����Ȥ�Ҥ٤Ƥ���褦�˸����ޤ���������֤���ϡפΤȤ��˸����غ����Ƥ���Τǡֿ��ذ��̡פ��äǤϤʤ����ȤDz�����Τ��Ȥ���äƤ���ȹͤ���������ޤ���
�����餯�����ϡʤ������ȤǤλѤ�������仡���Ƥ�˻�®�٤�ȯ��®�٤δ֤������γ����������ʪ���ȸ��������ޤ���ȯ��®�٤���®�٤����ڤ����٤����ᡢ������Ȥ������Τ褦���ä����ˤʤäƤ��ޤ��ΤǤ��礦���Ǥ�����ȯ������������ʬ���������Ƥ����Сָ�����Ȥ�ʤ��Ȳʤ��Τ˲���Ф��Ƥ��ʤ��Ƥ��פΰ�̣��狼�äƤ����ʤ����Ȼפ��ޤ���
�ǡ��ޤ��ϡָ����פ����ꤹ�뤢���꤫�顣�ʹߤʤ����������ٶ��Ρ��ȡʾС��ˤߤ������ä�³���ޤ�...��
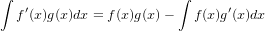
���Ѥ���ʬ����ʬ��ʬ�ˡ����ȸƤФ���ĤǤ������դ���ʬ������̤Ǥ��뱦�դˤޤ���ʬ���ĤäƤ���Τǡ���ʬ����ʬ�ȸƤ֤ߤ�����
���ơ��ͤФʤ�ʤ�����x^{2}logx��x^2��logx���Ѥȸ��ʤ�����ʬ���褦�Ȥ����硢���줾�����̤���ʬ���Ƥ���ñ��˳ݤ���碌��Ȥ�����ˡ�ϻȤ��ޤ�������ʬ�ϡ������פȤ�����������ĤΤǡ��¤�����ʬ������ʬ���¡פʤΤǤ������Ѥ�����ʬ������ʬ���ѡפǤϤʤ�����Ǥ������Τ��ᤳ�θ�����ɬ�פˤʤ�ޤ���
�Ȥ����ǡ����⤽��ʤ�ǡ��Ѥ���ʬ�פȤߤʤ��ΤǤ��礦����������f'(x)=x^2�����g(x)=logx�ȸ��������ƤϤ�Ƥ��ޤ���������ˤ�ä�logx����ʬ���ʤ��ǺѤ�Ǥ��ޤ��ʢ������logx����ʬ��ޤ��Ѥ���ʬ����������ư�������ꤽ���Ǥ�����������Τ�ˤ��п�����ʬ�ˤĤ��Ƴ�ǧ���Ƥߤʤ��Ȥ����ޤ��Ǥ⤽�η�ϤȤꤢ������ˤ��ơ������ʬ��ʬ����������Ω���ʡ��ˤ�����Τ���ޤ���
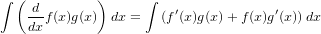
��Ҥ���������f(x)g(x)���դ˰ܹष����ʬ��ʡ��ˤ��դ˸Ǥ�ޤ��������ˡ���ʬ���¤��¤���ʬ�פȤ������Ȥ��鱦�����Τ���ʬ������ˤ��ޤ����ޤ����դ�f(x)g(x)����ʬ����ʬ���Ƥ���ȹͤ��뤳�Ȥˤ��ޤ��ʢ���ʬ����ʬ�ϸߤ��˵մؿ��ʤΤ�...��ǰ�����Ȥ����櫓�ǡ��ʤ�ȡ��Ѥ���ʬ���������Ρʡ��ˤϡ��Ѥ���ʬ�������ä���Ǥ��͡�
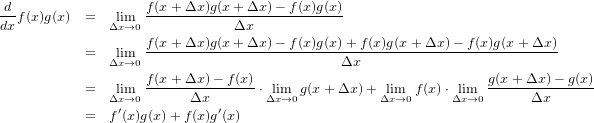
������Ƴ���Ф��������ñ�˽Ф��Ƥߤޤ�����2���ܤˤ��̾Ρ�˷����Υ��Сסʡ��ˤȤ������ٹ��Ƥ��ޤ��������������䤹�����뤿��˲��������ư����ʢ��Ĥޤ�ץ�ޥ��������ߤ����ʡ����ͥ��ϡ���������Ȥ�������ʬ�١���¼ʿ,2004�ˤ�p.63������Ǥ������¤ζ˸¤϶˸¤��¡פǤ����Ʊ���ˡ��Ѥζ˸¤϶˸¤��ѡפǤ⤢��Τǰ쵤�ˤޤȤ��3���ܤΤ褦�������Ǥ��ޤ���
�������Ƥߤ�Ȥɤ������Ѥ���ʬ������ܺ٤˳Ф��Ƥ��ʤ��Ƥ���Ѥ���ʬ���������꤫����é�äƤ����м��Ϥ�Ƴ�ФǤ������Ǥ����������ŵ����Ƥ��������ä��ᤤ�Τǡ������������Ȥǻ�İ�Ԥ�¾�νб�ԡ������åդ����Ǥ���ʤ����֤ǥ��äȲ��Ȥ��θ���ơָ����ʤ�Ȥ��Ф��Ƥ�Сפȸ��ä���ʤ��Ǥ��礦���������ƻ��֤����������̵���ΤǤ���С��������狼��в��ˤ�Ф��Ƥʤ��Ƥ��פȤ����ä��ȡ�
���ơ������ĥ�ä��п�����ʬ���äȤ��ޤ���...�ʢ���ε�̳�����С�������¼��2004�ˤ�pp.38-40������ͤˤ��ޤ�����
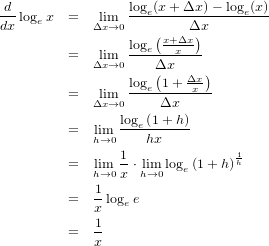
�п��Ǥ����̡ʡ��ˤδؿ����Ȥ���Ʊ���˷����Ƥ����ޤ����п��κ��Ϥ��줾��ΰ����ʡ��ˤξ��ˤʤ�Τ��ʢ�����פ������������ɽ����...�������2���ܤΤ褦�ˤʤ�ޤ���4���ܤǤϦ�x/x=h���֤������Τ���ؤ��ޤ��������ΤȤ���x��0�ʤ�Ц�x/x=h��0�ʤΤǶ˸¤β��Υ�ġʢ����ˤ⤽��ʴ������ѹ����Ƥ��ޤ���
5���ܤ϶˸¤α�¦�ʡ��ˤ��п���1/hx���Ѥȹͤ������1/hx��1/x��1/h��ʬ�䤷�Ƥ�����Ѥζ˸¤϶˸¤��ѡץ롼��ʡ��ˤˤ�ä�1/x�Ȥ���¾��ʬ�䡣�п��η����ϰ������߾�ˤʤ�ΤǤ���ʴ����ǽ�����
���ΰ�����ʬ���(1+h)��1/h��פ�h���¤�ʤ�0�˶�Ť��Ƥ����Ȥ����Τϡ�1�˸¤�ʤ������������ͤ�ä�����Τ�̵�²��߾褹��פȤ�����̣�ˤʤ�ޤ��ʢ�����h����ξ��⤢�ꡢ���ΤȤ��ϡ�1�˸¤�ʤ��ᤤ���ɤ���äȾ������ͤ�̵�²����Τεտ��פȤ�����̣�ˤʤ�ޤ�...1/h����ˤʤ뤫��Ǥ���...���������ȡ����Υͥ��ʡ��ˤ��ޤ˿���ƸĿ�Ū�ˤ��ä����ۥå��ꤹ��ʤ����ȴ����Ƥ��ƤȤäƤ���Ǥ��ʢ����ˡ�̵���ϡʤल�������ˤ����ޤ����ȳ�Ȥ����Ǥ�ʤ���Ʊ���˸���Ƥ���Ȥ����ޤ���...���ۤܡ�1�פ�̵������2.71828...=e�פޤǤ�äƤ����ΤϳΤ����������ɡ��Ǥ�2.7����äȤ�...̵�¤ʤΤ�...�ߤ����ʡʾС�����
�п����줬e�ʡἫ���п��ˤΤȤ�������Ʊ����e����1�ˤʤ�Τ���ʬ������̤�1/x�Ȥ�������ץ�ʤ�Τˤʤ�ޤ�������ޤ����Ѥ���Ф��Ĥ�����ڤˤʤ뤫�ɤ������Τ�ޤ������ʤ��Ȥ�����Υ������Ǥ����Ω�äƤ���褦�Ǥ�����
���ꤵ�줿�������˥���ץ�Ǥ����������ˤ����äƤϡ������طʡס֤��ä�����İ�Ĥ��ä��ꤷ�������פȤ��ä���Τ�狼�äƤ��ʤ���Фʤ�ʤ����Ȥ���ǧ�Ǥ��ޤ������ޤ��ˤ��ä�����̤�Ȥ�������������������Ū�ǥ��ꥢ�ǰ������ޤ��̵���פȤ�����ʬ�ˤĤ��ƤϤ��դ�ʸ�ϴ�ǤߤƤ��뤳�Ȥ����ݤ�ü�ޤä��ʢ�����ʬ�������Ǥ���������˸¤������ˤĤ��Ƥξ������ͥ��ԥ������ФƤ���Ȥ����Υ��쥳����������������餱����ꥬ�饹���λ볦�ǽ�ʬ�˳�ǧ�Ǥ��ޤ���Ǥ�����������Ϥ��ä�������ʤΤǥ���Ǥ���
���������ȡ��Ĥ��ǤȤ������������Ȥǵ��ˤʤä����Ȥ����ä��Τǥ��ޥ��ǽȤ��ޤ�������ϵ�������ʬ�ˤĤ��ƻʲ�Ԥ��������Ƥ���Ȥ��˲��̤˽Ф��ƥ��åפʤ�Ǥ�����...��
����ƥ�������ʬ���ޤ�����ʬ������פθƾ�
�ʤ��Ƴ�ï�Ǥ⸫�Ф��Τ���֢�����contour integral���ѤΥ����ʢ�����ʹ��١��ʵ���Ȥä����Ȥʤ��ʥ�...������㤨���Τ����ʲ�Ԥ�¾�νб�Ԥ��礲���˥Х��äݤ�����äƤ����Τϱ�Ф��ʡ��ȻפäƤޤ�����������ץ����Ǥ���ʤ��Ȥ����̣���狼��ʤ��ƥ��磻...�����ʰʲ����ȡ�
>> Definition:Contour Integral��Proof Wiki��
���������ʬ���ä����ˤ��Ȥ��ޤ�������...�������UFO�������ʢ������äƤߤ�ȡ�UFO�٥��ȥ�פϥҥåȤ����ΤΡ�����ñ��ϸ��Ĥ���ʤ�...�����㤤����...��������ˤĤ��Ƹ��Ȥ�������Ϥ���������Ƥޤ���ƻ̱�����������Τ˻ȤäƤ��������ȵ��ʤ�Ǥ�����������������ϥ����������Ȥ��ä��Ȼפ��ޤ���ʸ�Ϥ����ˤ���������ؤ�ƻ�����ȼ���Ū�ʰ�̣�ǡ�
�ǡ�����ʬ�ˤĤ��Ƥ�ޤ�����������ʤ��Τǰʲ�;�Ϥε����¤�������ʢ����ˤĤ��Ǥ��������νФƤʤ����ʢ����������ʸ��Ǿ�Ǥ�...�ΰա��ʤɤ�ޤ�ǡ�
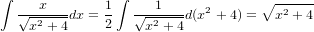
�����ȡ��ǽ�˸��ڤ����嵭�μ���⤦�������ͥ��ͤ��Ƥߤޤ���
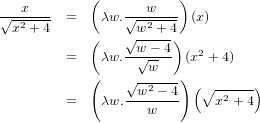
��ʬ���븵�δؿ��Ǥν�°�ѿ��ʢ�����Τ��Ȥ�ִؿ��פȸƤ֤��麮�𤹤�Ȼפ��ΤǤ���...���ο����Ȥ��Ƥθ�������Ʊ���Ǥ��äƤ���Ω�ѿ�������ǡ���Ǵؿ��λѤ��Ѥ�뤳�Ȥ�������dz�ǧ���Ƥߤޤ���������ʬ���оݤϽ�°�ѿ��ǤϤʤ������ޤǴؿ��ʤ櫓�Ǥ���������ʬ����ǽ���ɤ�������Ω�ѿ�������ˤ�ä��Ѥ��ޤ����������ִ���ʬ�פʤɤȤ��ä�ʸ�����֤������Ʊ����Ȥ������ʢ���ʬ�ǻȤ��ֹ����ؿ��פǤ�ʸ�����֤������ʤɤ�Ʊ�͡��ˤ���Τϲ������ⲽ���Ƥ���ȤޤǤϤ����ޤ��������γؽ����ʢ��㡧����������������礭��˸����ΤǤϤʤ������ȴ������ޤ������ܼ�Ū�ˤϴؿ��ι�¤�ʡ��ˤ���Ω�ѿ��������Ѵ�������ʬ��ǽ�ʤ�Τ˺Ʋ�᤹��Ȥ����äʤ�Ǥ���͡�
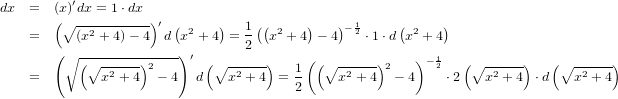
dx�ˤĤ��Ƥ�Ʊ�ͤΰռ��ʡ��ˤ�Ĵ�٤Ƥߤ�Ⱦ嵭�Τ褦�ʤ��Ȥˤʤ�ޤ���1���ܤ�x=x��x����ʬ����dx����Ƥ��ޤ���2���ܤǤ�x=\sqrt{(x^2+4)-4}��(x^2+4)����ʬ���ʤ���Фʤ�ޤ�����ʡ��ˤ��ˤޤ��ľ�ܤ���ʬ�Ǥ��ޤ���3���ܤΥ�������Ʊ�ͤǤ���
�����Ǻ����������뤿��˺�����ʡ��ˤο�����Ʊ�ͤΤ�Τ�Ȥä���ʬ���ޤ������η�̤�2��3�Ԥˤ�������ܤ����汦�ξ軻�����ʬ����줿�����κ�ü�֥��å��Ǥ��ʢ����������������ޤ�������Ʊ����¤�ʡ��ˤ���ʬ��Ԥä��Τ���Ӥ���ȷ����Ȼؿ������פ��Ƥ��ޤ���
���٤Υ֥��å��ʡ��ˤϤ��ΤȤ���ʬ�˻Ȥä�ñ�̡ʡ��ˤ��㤨��2���ܤʤ�(x^2+4)�ˤ�����������ʬ�˻Ȥ������ä��ѿ�����ʬ������̤Ǥ�����ü�֥��å��Ȥ��α��٤��Ѥ���������ä���ʬ��̤ˤʤ�ޤ���(dy/dt)(dt/dx)=(dy/dx)�Ȥ����ֹ����ؿ��פθ����̤ꡣ��֤֡ʤ����ʬ���ѤʤΤˤ��Τޤݤ��Ƥ�Ρ����פȸ��������ʤ�ޤ����ʢ��ʤ�ޤ��������Ǥ���...��ξ�Ԥΰ㤤���㤨�аʲ��Τ褦�ʤ��ȤǤ���
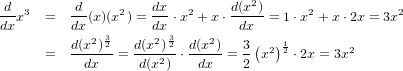
���Ѥ���ʬ�פǤ���ʬ�˻ȤäƤ�����Ω�ѿ���Ʊ��Ǥ����ֹ����ؿ��פǤ�����ब�Ȥ��Ƥ��ޤ�������˸¤餺Ʊ����̤˻��ۤʤä���ˡ��¸�ߤ��뤳�Ȥ�����ʬ�Ǥ϶���ξ��ʤ��롼������ǽ�ˤʤ��ʢ����ˤβ�¿����������ΤȤ���...���ΤǤ���������ˤϤ�������ѥ���Τ褦�ʻ����������ǽ�ʼ��ʤ����Ѥ���ޤʤ��ƤϤʤ�ޤ������������Ȥ������������Ǥʤ����Ȥ����ΤϽ������礭���ƶ������������ʤ�...�ȥѥ�������μ��Ȥ��֤ä�ί©��Ĥ��櫓�Ǥ������ʢ����ؤ����դʿͤϳ��ͥѥ��빥���Ȥ�������...����
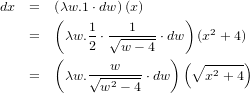
dx�ˤĤ��Ƥ����������Ω�ѿ��˱�������¤�ʡ��ˤ�ޤȤ�Ƥߤޤ��������Υ������ˤ��ޤȤ�ȹ�碌�Ƥߤ�ȼ¤���Ω�ѿ���\sqrt{x^2+4}�Ȥ���3���ܤ��Ǥ���ʬ�����ڤˤʤ뤳�Ȥ��狼��ޤ�������ʴ����ǡ�
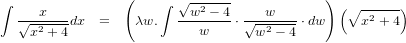
�Ȥ����Ǥ����ޤǥ��ͥ��ͤ��Ƥ��������������Τ褦�ˡ��Ѥ���ʬ�פDz��Ȥ�����ɤ��ʤ�ΤǤ��礦�������ξ��Ϻǽ������ʡ��ˤ�x��1/\sqrt{x^2+4}�Τɤ������ʬ�Ѥߤȸ���������2����Υ롼�Ȥ�¸�ߤ����ޤ���
�ǡ���äƤߤ���̤��餤���ȡ��ޤ����⤽�����Ȥ��ơ֤���������Ѥ���ʬ�ϥ����פǤ��ʾС��ˡ��ɤΤߤ��������ǡ��ִ���ʬ�פ�ɬ�פˤʤ뤷���ä�1/\sqrt{x^2+4}����ʬ�Ѥߤȸ������ʤ�����ʬ���Ȥ��ʤ�����ʤ�ʤ����Τϥѥ��빥���ˤϴ���ʤ��ʢ�����Ķ�����롼�Ȥȸ��äƤ褤�Ǥ��礦��
>> �ü���ִ�������ʬ�ʼ����η��
����ؤ��о줹����Ǻǹ����٤���ʬ�ѥ�����Ǥ���
�ǹ����٥������졣���ʤߤ˾嵭�Ϥ��Ф餷�����ͤˤʤ륵���ȤǤ������꤬�Ȥ�����¿���졣�ǡ������ǾҲ𤵤�Ƥ�����ˡ��Ƴ�����Ƥޤ��������ˤޤȤ�Ƥߤޤ���
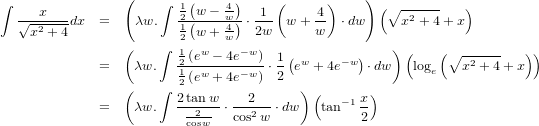
�����˻�����β��ʡ��ˤ��ä��ޤ����ʤˤ��Ƥ���Ƥ��...�Ȥ��������ʤ�ޤ����ʢ��Τ��˺�����¿�༰�Ȥ�����ʬ�ξ㳲�Ͼä��Ƥޤ����ɤ�...�����ĤȤ��طʤˡ��ж����פ�ͤ����祤�����뤳�Ȥ餷�������ʤߤˡ��ж����ؿ��פϡ��ؿ��ΤϤʤ��������١���¼ʿ,1977��pp.200-208�ˡֻؿ����п������Ѥ���ر��δ��פΰ���ܤȤ��ƽФƤ��ޤ����ΤǾ��ʤ��Ȥ�70ǯ����������Ǥ���ؤɤ�������ر��ǰ������Ƥ��ä��ߤ����Ǥ������٤�����ǤϤʤ�ñ��ͥ���̤����Ǹ�ˤ���Ƥ����������⤷��ޤ���
��ع��ǽ��ä����㡦ȿ����Τ������Ԥϰ켡�ؿ����ؿ�������ȯŸ�ʡ��ˤ��Ƥ����ޤ���ȿ����ʡ��ж����ˤ����Ϥ��ޤ�¸�ߴ����ʤ��ä��褦�ʡ��פ��Ф��Ƥߤ�ȿ�����ɽ�����㤨��y=1/x�ߤ����ʤ�Τǡ�x=0�ΤȤ�y���ͤ�¸�ߤ����ʤ����ʢ����������ˤʤ뤿�������դ���Ĥ�ʬ���ʡ��ˤȤ��Ȥ���
�����ж����Ⱦ�ǽ����Ĥμ����ɤ��Ҥ���Τ��ϥԥ�Ȥ��ޤ������Ǽ���ʡ��˰���ͽ��ε��ѡʢ����ˤ�Ȥä�y=1/x��45�ٲ�ž����ĺ���ʡ��ˤ�(0,1)�ڤ�(0,-1)�ˤ�äƤ���褦���Ѵ����Ƥߤޤ������ִ�ؿ��פǤ��ä�y=1/x��y�����оΤʡֶ��ؿ��פ��Ѵ��������Ȥ������ȤǤ����Ȥꤢ�����������Ƥߤ褦���Ȥ������Ȥǡ�
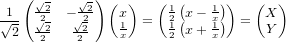
����äݤ���Τ��ФƤ��ޤ������Ѵ��˻Ȥ�������ʬ����������y=4/x�ξ���ȼ��Τ褦�ˤʤꡢĺ���ʡ��ˤ�(0,2)��(0,-2)�Ǥ����ж�����ɽ���Ƥ���Ȼפ��ޤ���
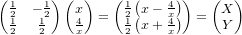
���Υ�������X��x��ɽ���褦���ѷ����Ƥߤޤ��礦��
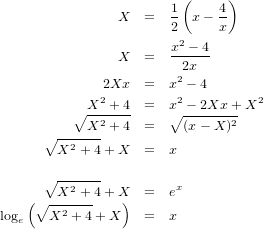
����鸫���褦�ʤ�Τ������ԤΤ��ȤĤ��Ǥ˻ؿ��ؿ���Ȥä����ˤĤ��Ƥ��ʤ��ξ�η�̤�����Ѥ��ơ���äƤߤޤ������ܻۤ����褦�������ʡ��ˤ��Ȥ��Ƥ���褦�Ǥ���
���ơ�ñ�̱ߤ�X^2+Y^2=1�Ǥ���ΤȻ���ɸ���ж�����-X^2+Y^2=1��ɽ����Τ��Ȥ�������X��Y�����������٤�����Ρʡ��ˤˤĤ��ƹͤ��ޤ���
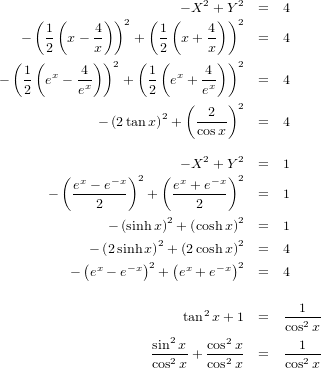
������Ŭ���˽��֤äƤߤޤ�����2����4���ܤޤǤ�1���ܤ�X��Y�˿�������Ƥߤ���̡ʡ��ˤǤ����츫�����4���ܤϾ�2�ԤȾ����㤤�ޤ���1/cos(x)��sec�ʡ�secant����������֤�������ȡʲ��ԤΤߤιԤ�����ơ�8���ܤ�Ʊ�������Ȥ����ޤ���sinh��hyperbolic sine��cosh��hyperbolic cosine�Ȥ����ж����ؿ��Ǥ����ʻؿ��ؿ����п��ؿ�����ӻ��Ѵؿ��Ȥ��ä�¾�ν�����Ķ�״ؿ���ޥ���������������Ȥη����礤�ˤĤ��ơ������ꤹ��ΤϤޤ����١ʡ��ˤȤ������Ȥǡ�
����Ǹ�Υ��ޥ�Ū�˻��Ѵؿ���Ȥä�ĶĶ���ɥ����Ǥ���ʬ����äƤ����ޤ����ޤ��Ϥ�Ȥ�Ȥ���ʬ��ʬ�ҡʡ��ˤ�x�������Ĥ��顣�ʤ����㥴����ˤ��Ƹ�äƤ��ޤ��������Υ����פ��̤˺���ؤ���ʤ���Ǥ���͡����ޤǸ��Ƥ����褦�˴�ñ�˲��Ȥ��ǽ�ʤ櫓�Ǥ����顣
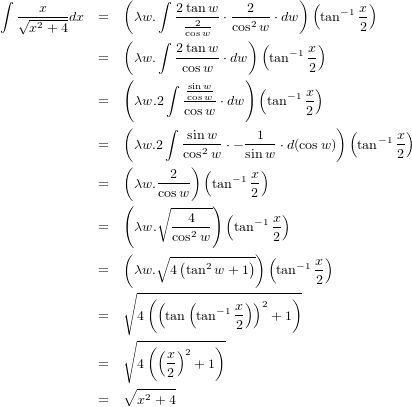
��������������Ω�ѿ���cos(w)�˴�������ʬ��ԤäƤ��ޤ����ޤ������ޤǤȤ��˸��ڤ��Ƥ��ޤ���Ǥ�����tan^{-1}�Ȥ����Τ�arctan�Τ��Ȥ�tan�εմؿ��ΰ�̣�Ǥ���1/tan�ȤȤ������ȤǤϤ���ޤ���
�����Ƥ��褤�輡���������ʹ���ˤȤäƤϡ��С���������������侩�Υ��ɥ�������ˡ����ʬ������ΤǤ������楹��ʥꤤ���ʤ���ʬ���ʹ��פǾ��ۤ��Ƥ��ޤ����Ǹ�ΤȤ�����+log_e(1/2)�Ȥ���;�פʤΤ��ܤ��դ��ޤ������������ʬ���C����ʡ��ˤ˴ޤޤ��ΤǤ����ޤǤΤ�����˽�����ɽ������̵�뤹�٤��Ǥ��礦���ʤ�Ȥʤ��Ĥ��ޤ�������
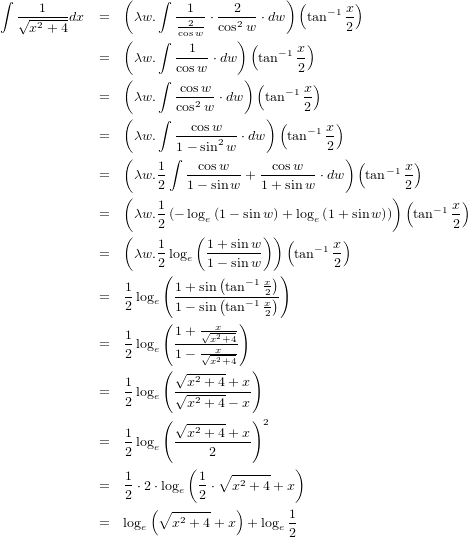
�嵭��ʬ�ǻȤä������ʡ��ˤ��������äȤ�����⡣�����ޤǥ��ͥ��ͤ�äƤߤ����ۤ��С���Ϥ�����ʬ���ä���ʬ�����դϥѥ���äݤ���...�Ĥޤ����ؤǤϥѥ���������̵ͭ�����Ƥ����Τ��ʡ��Ȼפ��ޤ��롣������ˤ����ȥѥ��뤬��Ω������ߤ����ʤ�Τ�������ɬ�פˤʤäƤ���褦�Ǥ�����������
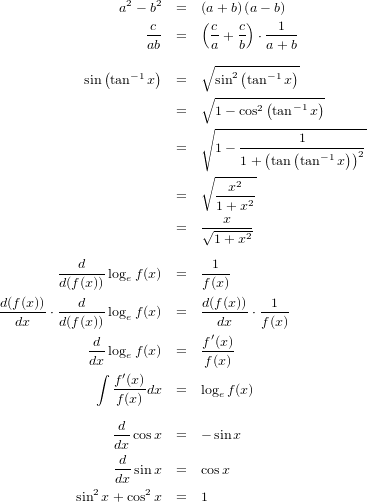
�Ȥꤢ��������ʴ����ǡ�

����ȯ�פȤ����������פˤĤ��Ʋ������ȥ��쥳�줷�Ƥ����ʤȤ������֥參������ʬ�����äƥ�˥�äƤ롧��������������˻��֤��вᤷ�Ƥ��ޤäƥ���ܥܥܡ��ǡ����Τ�������äϰ�ö�����֤��Ĥġ��Ƕḫ���ֳ�Ψ�פ�������ࡹ�˴ؤ��Ƥ���äȲ������äƤߤ褦�Ȼפ��ޤ���
>> ��Ψ�˴ؤ��ƤΤ��Ȥ���togetter��
���ڤ���ΤϾ嵭�ΰ�
���������ޤ��Ĺ��Ǥ�������鿧��������Ƥ���褦�Ǥ⤢�ꡢ������Ƕ�̣�ʡ��ˤ���ä���������Ū��ʤäƤߤޤ���
�ھ������㤨�С�����������6000�ä��Ȥ����Ф��ܤο��Ϥɤ��1000�Ĥˤʤ�Ȥ����Τ����ؤ������˴�Ť������Ǥ������������ºݤˤ�äƤߤ��ʬ���뤳�Ȥ��������������ʥ��������Ǥ��äƤ�6000�äƤߤ�ȣ���998����1003�������Ȥʤ�Τ����̤Ǥ��äơ����٤�1000��Ԥä���Ȥʤ뤳�Ȥϵ��Ǥ����������ˤ��٤�1000�Ĥˤʤä��Ȥ��Ƥ⡢����϶��������ʤä��Ȥ��������Ǥ��äơ���Ψ���η�����Ʊ����̤Ȥʤä�����Ȥ��äơ����������Ρ��������פ�Ω�ڤ��줿�Ȥ������ȤˤϤʤ�ʤ���������ξ�ԤϤ����ޤǤ⼡����ۤˤ���Τ����顣��15 Oct 2015��
��Ĥ�Ϣ³����ȯ���äĤ��ޤ����������ϰ��ѼԤˤ��ޤ���
����ȯ���ˤĤ����ʤ��������Фʤ�Ǻ���2015ǯ��ȯ�������夲��줿�������...�褯�狼���...���ְ㤤�λ�Ŧ�����ä��褦�Ǥ��������Ǥμ�ĥ���Τ��դ�ʸ�Ϥ����Ǿ��ñ�㲽���������ʡ��ˤ��Ƥߤޤ��ȡ�
�֥���������6000�äƤɤ��ܤ�1000�Ĥˤʤ뤳�Ȥ�...��
(1)����Ū�и������Ǥϴ��Ǥ������������ܤβ������ˢ������̤�
(2)���ؤ������˴�Ť������Ǥ���ʺǽ�β������ˢ������������ؤǤ���ȷ�������
�Ȥ������Ȥ��ȡ�����Ū�ˤϰʲ��Τ褦��ȯ������Ƥ��ޤ������������twitter���������̾�Ͼ�ά���Ƥ��ޤ���
����Ū�˴��㤤����Ƥ���褦�Ǥ��������ؤ���������Ψ���Ǥϡ�6000���ꤲ�Ƴ��ܤ�����1000�Ĥˤʤ��Ψ�� 6000!��{��1000����^6����^6000}���ǵ����ơ�����Ϥ����ȷ����Ƥ��ʤ��ΤǾܺ٤�ʬ����ޤ��������㤤��Ψ�Ǥ�����17 Aug 2016��
�ɤ���θ���ʬ���������Τ����ʲ��Ǽ�ʬ�ʤ�˳�ǧ�ʡ��ˤ��Ƥߤ뤳�Ȥˤ��ޤ���
�֥���������6000�äƤɤ��ܤ�1000�Ĥˤʤ�׳�Ψ�Ϥɤ���ä��������ΤǤ��礦�������֤�(A)�֥���������6000�äƤɤ��ܤ�1000�Ĥˤʤ�ѥ�����������פ�(B)�֥���������6000�ä��Ȥ��˽и��ʡ��ˤ����ǽ���Τ������ѥ�������פdz��Ф�������������������Τ�����㴳�狼��ˤ������⤷��ʤ��Τǡ����Ȥǥ������4���ꤲ��ɽ����2�Ĥˤʤ��Ψ�ʤ�Ȥäƺ��ٳ�ǧ���Ƥߤޤ�����
�嵭(A)��(B)�˴ؤ��Ƥ��줾��ɤ���äƷ�����Ф褤�����狼��г�Ψ�Ϥ�Ȥޤ�ޤ����ǡ�(B)�ˤĤ��ƤϤ����狼���ʤ����ʡ�
�ǽ��1���ܤǵ����ꤨ��Τ�1��2��3��4��5��6�Τ����줫���ܤ��Ф�ѥ������ʤ��Τ�6�ѥ�����Ǥ���2���ܤޤǤ˽и�����Τ�1���ܤ�6�ѥ�����Τ��줾�줫��6�ѥ������ʬ�������ä�6^2��36�ѥ�����ˤʤ�ޤ���Ʊ�ͤ�3���ܤ��ʳ��Ǥ�36�ѥ�����Τ��줾��ˤޤ�6�ѥ������ʬ�������뤫��6^3=1295�ѥ����Ĥޤ�6000�ä��Ȥ��ˤ�6^6000�ѥ�����Ȥ������Ȥˤʤ�ޤ���
�դ˸����Сʡ��ˤ���6^6000�ѥ�����ʳ��η�̤�¸�ߤ����ǽ���Ϥʤ����ºݤλ���ʡᤳ�ξ���6000��������Ȥ����٤�1���åȹԤ����ȡ��ǤϤ����椫���Ĥ����֤Ȥ������Ȥ��̣����Ϥ��Ǥ����ʤ�Ǥ��礦�͡���ή��������֤��Ȥ�6�ܤ�ʬ���������Ƥ�����äƤ����Ȥ�����ǽ���Ȥ��ƤϿ����ʥ롼�Ȥϼ�ꤨ�뤱��ɤ⡢�ºݤ�����η�̤Ϥ��������ܤ�ƻ�ˤʤäƤ�Ū���ʢ��������꤫������
�ޤ������������ν��ܤϤɤ��Ʊ����Ψ�Ȥ������Ǥ����顢6^6000�ѥ�����Τ��٤Ƥ�Ʊ���������Ψ�ʡ��ˤǤ��ꡢ�ͤ�1/��6^6000�ˤǤ���1/6��6000��ݤ��Ƥ���Ȥ������ȤǤ��͡��ǡ����줬6^6000�ġʡ��ˤ���Τ���������1�ˤʤ롢�ȡ���������̣�˲���������Ƥޤ����ʴ��ˡ�
����(A)�˼��ݤ���ޤ����Ȥꤢ�����֥���������6000�ä�1���ܤ�1000��Ǥ�ѥ�������פ���ͤ��Ƥߤޤ��礦���ȤϤ�����ݻͤ����ʤ���...Ʊ���褦�ʹ�¤�ʡ��ˤ��̤ζ���Ū���ä˰�ö�Ѥ��Ƥߤޤ���
�ֺ����鱦�ؤȲ��˥���äȥ����������Ȥ�꤬�����6000�ս��¤�Ǥ��ơ�������1���ܤ��ˤ�������������1000�ĤϤ����ѥ�������ʤ���������������ɬ�������鱦�ν�ǤϤ����ˡפȤ����Τ��ʼ�ʬ�ˤȤäƤϡ��С����狼��䤹�����ʡ�����ʤ����Τϡ�ñ�ʤ�6000�ս꤫��1000�ս��������Ȥ߹�碌��combination�ˡ����Ȥ������դ��ޤ����ֽ����permutation�ˡפ���ʤ��Τ�1000�ĤϤ���ޤ��Ȥ��κ�Ƚ���ʡ��ˤΥХꥨ������ֺ����鱦�롼��פˤ�äư�Ĥ˹ʤ��뤫��...�Ǥ����Τ��ʡ��ʢ����䤫����
�ǡ���1���ܡפ�1000����������ƥѥ�����ˤ����ơ��ޤ������Ƥ���6000-1000=5000�Ĥη���Ф��ơ����٤ϡ�2���ܡפ�1000��������ѥ������������ޤ���5000�ս꤫��1000�ս��������Ȥ߹�碌���Ȥ������Ȥˤʤ�Ǥ��礦��Ʊ�ͤˤ��ơ�3���ܡפ�4000�ս꤫��1000�ս������4���ܡפ�3000�ս꤫��1000�սꡢ��5���ܡפ�2000�ս꤫��1000�ս�����֤Ȥ��Ρ��Ȥ߹�碌���Ȥ������Ȥˤʤ�ޤ�����6���ܡפˤĤ��ƤϻĤä�1000�ս�������;��̵����ưŪ�ˤϤ���ޤ�뤿�ᡢ�ѥ�����������ˤϱƶ����ޤ���
�����ºݤ˷����Ƥߤޤ��ȡ��ʲ��Τ褦�ʴ����ˤʤ�ޤ���
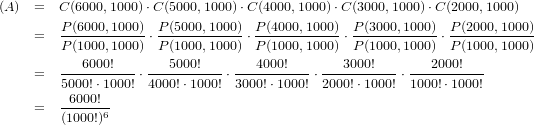
�ؿ�C(N,m)��N�Ĥ��椫��m��������Ȥ߹�碌�ץѥ���������֤��Ƥ����Τǡ�P(N,m)�ϡֽ���פξ��Ǥ����ؿ�C(N,m)��P(N,m)�ˤ�P(N,m)=C(N,m)��P(m,m)�Ȥ����ط�������ޤ���x�Ĥ��椫��y�����֤Ȥ��ν���ѥ�������˴ؤ���ؿ�P���̤ʻ�����ɽ�������P:(x,y)��x!/(x-y)!�ߤ����ʤ��Ȥ��ȡ���Ĥ���0��ޤ༫�����Ǥ�����ѿ����Ȥ��Ф���ͭ�����Ǥ����ͤ���Ϣ�դ����Ƥ���Ū�ʡ����ΤȤ�x��y�����Ǥ��͡��ޡ��ʤ��������ǥ���Ǥ�������
�������㤯�Ƹ��Ť餤�ʢ��פ��̤�ˤʤ��...kstexg���ޡ��Ǥ���(A)��6000!/(1000!)^6�Ȥ狼��ޤ����������(B)�η���̤Ǥ���6^6000��Ȥä�(A)/(B)=(A)��(1/(B))=(6000!/(1000!)^6)��(1/6^6000)�����Ǥ��ޤ��ʡ�7.8237477367814982E-10�פȤ��餷���Ǥ�����...E-10��10�Υޥ��ʥ�10�衢�Ĥޤ�1/10^10...100��ʬ��1��ݤ����Ȥ������ȤΤ褦�Ǥ�...100��ʬ��7.8�ʥ�ȥ��Ȥ������ȤǤ������å�����ä����ͤˤʤ�äƤ��Ȥ��ȡ���
���ä��������ޤ��������ɤ������ؤˤ����Ƥ�֥���������6000�äƤɤ��ܤ�1000�Ĥˤʤ뤳�ȡפϡִ��Ǥ���פȤ����������������褦�Ǥ���
������������ǤϷ�����䤳�����ä��Τǥ���ץ�����Ȥä�Ʊ�ͤΤ��Ȥ��äƤߤޤ�������Ū�ˤ�ɽ��Ʊ��Ψ�Υ������4���ꤲ��ɽ���Ԥä���2�Ĥˤʤ���ˤĤ���Ĵ�٤ޤ���
�ޤ������ꤨ�����ѥ��������ɽ2�ĤΥѥ�������ʳ�ʬ���褴�Ȥˡ�4������Τ�2^4=16�ѥ�����Ǥ������Τ���ɽ��2�ĤǤ���ѥ�����ϥ��������ΤȤ���Ʊ�ͤη���4!/{(2!)^2}=6�Ȥʤ�ޤ���
�����ʡ��ˤȤ��Ƥϡ֥�������Ȥ����4�Ĥη��ߤ�����˺����鱦�ؤ��¤�Ǥ���Ȥ���ɽ���ˤ����������2���Ȥ����ѥ�������פȤ����ͤ�����C(4,2)=P(4,2)/P(2,2)=4!/{(4-2)!��2!}=6�Ȥʤꡢ�ʥ��������Ǥ�����6���ܤΰ�����Ʊ�ͤˡ�ɽ�ΰ��֤���ޤ�ȼ�ưŪ���ΰ��֤��ޤ뤿�ᡢ���줬���Τޤ�ɽ2�ĤΥѥ�������Ǥ����������ʤ��ΤǼºݤ˽Ф��Ƥߤޤ��礦��
��������
��������
��������
��������
��������
��������
��ݤ�ɽ�ǹ��ݤ��ΤĤ��Ǥ������äƤ����櫓�ǤϤʤ��Ǥ������ʤ�ۤɥۥ�Ȥ�6�ѥ�����Ǥ��͡���Ψ�Ȥ��Ƥ�6/16=0.375�Ȥʤ�ޤ������̤ˡʡ��˶������ꤲ���Ȥ���ɽ��Ⱦ���Ȥʤ��Ψ��¸�ߤ���Τǻ�˾���¾������Ƥߤޤ���
2��2/4=0.5
4��6/16=0.375
6��20/64=0.3125
8��70/256=0.2734375
�ʡ����äƤ���Τǡ����֤�6000���ꤲ���Ȥ��ˤϤ�Τ������㤤��Ψ�ˤʤ�ΤǤϤʤ������ʤ��ʤߤ˥��������ξ�硢6�äƳ��ܤ�1�ĽФ��Ψ��720/46656=0.01543209876...�ʤΤǽ��ü���饳��������ʬ�㤤�Ǥ�...�����¤�Ʊ�ͤΤ��Ȥ�ְִ㤤�λ�Ŧ�ԡפǤ����ʪ��tweet���Ƥ��ޤ���
�⤷�����ơ���Ω�ʡ���ʸ�ޥޡ����֤�ֳ�Ψ�ס��γ�ǰ���Τ�Τ����Ƥ��ʤ������뤤�������ˡ§����Ƥ���Τ��⤷��ޤ��� �������������ꤲ��Ȥ��ơ�ɽ���ꤲ�����������Ⱦʬ�ˤʤ��Ψ�ϡ�������礭���ʤ�Фʤ�ۤɣ��˶�Ť��ޤ����Ǥϡ����٤ⷫ���֤������Ψ�̤�η�̤ˤʤ롢�Ȥ�������θ����Ȥϲ����Ȥ����ȡ� ɽ���Ф�������ꤲ������������ͤ����ꤲ�������礭������Ф���ۤɣ������ˤɤ�ɤ��Ť���̵�²�ʤ�����Ԥä��꣱�����Ȥʤ��Ȥ������ȤǤ�����20 Aug 2016��
�ֻ��ϰ��Ѽ����ʡ��ˤǤ���������twitter��������ȤϾ�ά������Ĥ�ȯ����Ҥ��Ƥ��ޤ��������ϰ��ѼԤ��դ��ޤ�����
�ǽ�β������ˤ���ޤǽҤ٤Ƥ����褦�ʤ��Ȥ���Ŧ����Ƥ��ޤ���������Ⱦʬ�ˤʤ�ץѥ���������Ȥϡ��ꤲ������פ��礭���ʤ�ΤˤȤ�ʤäƵ���ˤʤäƤ����ΤǤ����������ꤨ�뤳�Ȥ����ѥ����������������ʾ�Υڡ��������礹�뤿�ᡢ���Ԥ��Ԥdz�ä��ͤǤ���ֳ�Ψ�פ�0�˶�Ť��Ƥ������Ȥˤʤ�ΤǤ��礦��
�ޤ�������ܤβ������Ǥϡ�����θ������ʡ�������ˡ§�ס����������Ƥ���Ƥ��ޤ�������ˤĤ��Ƥϡ������λ���������ɴ���١ʿ��ض��鶨�IJ�2005�ˤβ��⤫��������Ѥ��Ƥߤޤ��礦��
�֥��������ä�1���ܤ��Ф��Ψ�פ�1/6�Ǥ���������������ϡ�6���ɬ��1��1���ܤ��Ф�פȤ������ȤǤϤ���ޤ���1���Фʤ����Ȥ⤢�뤷��2��3��Ф뤳�Ȥ��äƤ���ޤ�������Ǥⲿ��⿶��³����ȡ�1���ܤ��Ф����1/6�˶�Ť��Ƥ����ޤ������줬�����ˡ§�ǡ�����Ū�ˤ����ȡ���¿�����֤��С������������������Ψ�˶�Ť��פȤ������ȤǤ�����p.208��
�ɤ���餳������ͤ�¿���褦�Ǥ������������������ȸ���ͤ⤤��Τ��ʡ��Ȥ������⤷�ʤ��Ǥ⤢��ޤ����ʸĿ�Ū�ʿ�¬�Ǥ��������θ����ΤҤȤĤϡ����⤽���ʬ���פ�������ʳ������꤬����ͤ��¤ϰճ���¿�����Ȥ������Ȥ������ǤϤʤ�����...ʬ������Ǥ��뤳�Ȥ��ԥ�Ȥ��Ƥʤ��ơ��ޤ����ܸ�Ǥϡ֥ʥ˥���ʬ�Υۥ��ۥ��פߤ����ˡ�ʪ��Ū��¸�ߤ��Ĥ���ʬ�䤷����ΤΤ����β���ʬ�������̣����褦�ʸ�������Τ⤽�����֤��Ƥ���褦��...�֥��ʥ��֥��參�ƥʥ��͡��פȤ����������ݤȤ�����������ʤ����ʤ�...������¿�����֤��С������������������Ψ�˶�Ť��פȤ����Ȥ��Ρ���������Ψ�˶�Ť��פ������������˶�Ť��פ�Ʊ�����ȴ��㤤���Ƥ��ޤ����顢�äƤȤ��Ǥ��礦�����ʲ���;�פʤ����äǤ��礦����ʤ���������ߤƤߤޤ���
�����ȡ�4������ꤲ���Ȥ���ɽ�ѥ�������鱦�˿��Ӥ�����ޤΤ褦�ʤ�ΤȤ��ƥ�������Ƥ�����������ü������Ԥ�ʬ����Ƥ����褬��ɽ�פȡ��פ��̣����Ρ��ɤˤʤäƤ��ơ�������ĤΥΡ��ɤ��餽�줾��ޤ�Ʊ�ͤ�ʬ�������ä�...�Ȥ��������֤����4��ԤäƷ��������ޤǤ���
�������4���ꤲ��Ȥ����٤ϡ����οޤν�ȯ������3�ĤΥΡ��ɤ��ͳ���ƹԤ���4�Ĥ�ΥΡ��ɤ���ü��ã���뤳�Ȥ�Ʊ���Ȱ����ޤ�����ȯ��������ü�ޤǤη�ϩ�ѥ������16���äơ����Τɤ�⤬4�ĤΥΡ��ɤ�ޤߡ��Ρ��ɤ�����Ϥɤ���1/2�Ȥ�����Ψ�Ƕ����˹Ԥ��Ƥ������ᡢ16�����ϩ�Τɤ줬����뤫�γ�Ψ�ϰ�Χ��(1/2)^4=1/16�Ǥ���
���μ����ޤǥ������ȤǤ�ʬ������ˤ���Ρ��ɤ�Ĥˤߤ�ȡ�ɽ�פȡ��פο���Ʊ���ˤʤäƤ��ޤ������������Ǥ���...ɽ����1�Ĥ��ĤǤ�...��������2�ĤΥΡ��ɤ���ɽ���ʬ������ü�Ȥ���������4�Ĥ��¤�Ǥ���Ȥ����Ǥ�ɽ��������ɬ��Ū��Ʊ���Ǥ������ι�����ˤ�8�ĤΥΡ��ɤ�����ޤ�������Ʊ�ͤ���ͳ��ɽ��Ʊ�����Ǹ���¤�Ǥ���Ρ��ɤ�Ĥ˸����ɽ��Ʊ���ˤʤ�ޤ���
��ɤ��μ����ޤ˴ޤޤ�Ƥ���ɽ���ΥΡ��ɿ�������Ʊ���Ȥ������ȤǤ���
�䤿�����ºݤ˥������4���ꤲ��ȡ����μ����ޤ��鱦�ؤȥΡ��ɤ��ʼ�ʬ�ΰջפǤϤʤ���Ψ1/2�Ƕ����ˡ����ʤ����ư���Ƥ����ΤǤ��������ΤȤ��̲᤹��Ρ��ɤ�ɽ��Ʊ���Ȥϸ¤�ޤ������Ρ�����ӳ��ʳ��ǤΥΡ��ɽ������Ǥ�ɽ��Ʊ���ʤΤǤ�������ư��ϩ�˱�äƲ������˸����Ȥ���ɽ��Ʊ���ˤʤ��ݾ������̵���ΤǤ���
��ǧ���Ƥߤޤ��礦��
ɽ��1�Ĥ����ξ���C(4,1)=4��4�ѥ�����2�ĤΤȤ��Ϥ��Ǥ˷������褦��6�ѥ�����ɽ��3�Ĥ���1�Ĥȸ����������ޤ��ʡ��ˤ���4�ѥ����������̤˷����Ƥ�C(4,3)=4�Ǥ����������ޤǤ�14�ѥ����Ĥ����Ĥ�����ɽ�ξ��������ξ��γ�1�ѥ�����Ǥ���
�ƥѥ�����ϰ�Χ1/16�Ȥ����и�Ψ�Ǥ����顢
ɽ0��(1/16)��1�ѥ�����=1/16=0.0625
ɽ1��(1/16)��4�ѥ�����=4/16=0.25
ɽ2��(1/16)��6�ѥ�����=6/16=0.375
ɽ3��1Ψ�ʤΤ�0.25
ɽ4��0Ψ�ʤΤ�0.0625
�Ȥ�������ʬ�ۡʡ��ˤ��ޤ������ʤߤ�6���ꤲ���Ȥ��ˤϰʲ��Τ褦�ˤʤ�ޤ��ʸ�Ⱦ���Ͼ�ά���ޤ���...����
ɽ0��0.015625
ɽ1��0.09375
ɽ2��0.234375
ɽ3��0.3125
���礦��Ⱦ���ΤȤ����ϳΤ��˥ܥ�塼�ॾ����ʡ��ˤߤ����Ǥ����ɡ��ꤲ������������ȥѥ������ʬ�ۡʡ��ˤ��ФäƤ����ΤǤ��켫�Ȥγ�Ψ����ä��㤯�ʤäƤ���������
������ɽ�γ�礬1/2�˶ᤤ��ϩ�ѥ����ϡ������ǤϤʤ��ѥ�������Ф����ʷ��ߤΤ������ɽ�������Ϥ���ॱ�����Ǥ�¿���Υ������ʲս�ˤϤ��Ȥ��ۤ������;�Ϥ��礭�����Ȥ߹�碌�������礹��褦�ˡ��Хꥨ�������¿��¸�ߤ��ޤ��ʰ�����ɽ�γ�礬0�Ǥ���褦�ʷ�ϩ�ѥ�����ϥ�������ꤲ�������ɤ���������Ƥ�1�ѥ���������ޤ���...�դ�0�ѥ������Ʊ�ͤǤ�...�Ĥޤ�ξ��Ⱦ���ΤȤ����¤���������褬����ˤʤ�櫓�Ǥ�...������äơʡ��˥�������ꤲ���������礵���Ƥ����ȡ�ɽ�γ�礬1/2�˶ᤤ�ѥ������ºݤ˷�ϩ�Ȥ���������Ψ���夬�äƤ�����ֵ����������������Ψ�˶�Ť��פȤ������ȤǤ��뤬������������礬1/2�ˡֶᤤ�פȤ����Ȥ��μºݤ�ɽ�ο���Ⱦ�����饺��Ƥ����ٹ礤�Ϥ��ä������ȤˤʤäƤ��äƤ������衢�äƤ��Ȥ��ȡ�
�Ѥʤ��Ȥ��Ǥ�����20�Ф�10�Фȷ뺧�����͡�ex.�ᤤ�ͤ����������ȡ��ޤġˤη뺧��10��¦��ξ��ǯ���������ʡ��ˤ�10/(10+20)=1/3=0.333...�Ǥ��������οͤ�100�Фˤʤä������Ǥ���100/(100+110)=0.476...�Ȥ������˳��Ȥ��Ƥ�1/2�˶�Ť��Ƥ����ޤ���10�Ȥ����������ıƶ����������ʤäƤ��äƤ����Ǥ��͡�20�Ф�10�Фϡֶᤤ��ǯ��Ȥϸ���ʤ��Ȼפ��ޤ����ʢ��ɤä�������衢�դ��դ��դ�...�Ȥ���Ω��⤢�ꤨ�ޤ��뤬...������110�Ф�100�Фʤ�ֶᤤ�פȴ������ʤ��Ǥ��礦���������ޤǤ����ȥ��ͥ���Ͽ�Ȥ��ʹ֤μ�̿�θ³��Ȥ������꤬���äƥ���Ǥ��������ޤ���Ʊ���ǤϤʤ����ɡ�����Ȼ����褦�ʡʢ����ˤ��Ȥʤ�ʤ��Τ��ʤ�...��
���Τޤޡ֥����֥顼�κ������ʢ������פ�Ϣ³�����餽�θ�ϡ�Ⱦ�פνи�Ψ���������͡��ߤ����ʥ�ġ��˴ؤ����äʤɤ�³���Ƥ��ޤ��Ȥ���ޤ�ˤ�Ĺ���ʤäƤ��ޤ������ʤΤǡ��ޤ��⤦�����ֳ�Ψ�פˤĤ��Ƹ����������Ȥ��ĤäƤϤ��ޤ������ͥ���˷���ۤ����Ȥˤ��ޤ���
����DOT����Ǽºݤ˺�ޤ��Ƥߤ�ȡ���Ĺ�ˤʤ�Ĥ����ä������ޤ��Ĥ�Ĺ���ʤäƤ��ޤäƼ��ޤ�ȻȤ����꤬������...�Ȥ���ͽ�۳��ʢ�ͽ¬��ǽ���...jk���Υ������ǥ�ȡʡ��ˤ⤢�äơ��ޤ������ڤ�ľ���Ǥ���
���ʤߤ�DOT����ˤĤ��Ƥϰʲ��Υ����Ȥͤˤ����Ƥ�餤�ޤ��������꤬�Ȥ��������졣�������ޤ��ޤ������Ȼ��ͤˤǤ��ƤϤ��ޤ��ʤ��ߤޤ��ߤޤ���...��
>> Graphviz��dot����ǥ���դ�������ˡ�ΤޤȤ�
�ǡ�����ߤƤ��������ࡹ�κ��ܸ����ˤĤ��Ƥʤ�Ǥ����ɡ�
(1)�֥���������1���ܤ��Ф��Ψ��1/6�Ǥ����
(2)�֥���������1���ܤ��Ф�Τ�6���1��Ǥ����
������Ĥ�Ʊ�����Ȥ���äƤ���ȹͤ��Ƥ��ޤ��ͤ��빽�������롢�äƤȤ����ˤ��ä���ʤ����Ȼפ��ΤǤ���
(1)�Ͽ��ؤǤ⸽��Ū�и������ʡ��ˤǤ⿿�Ǥ���̿��ʤ�Ǥ����������(2)��Ʊ����̣���ȿ����Ƥ���ͤϡֿ��ؤ����äƤ�ߤ�����6���1��ʤ��ơ��и�Ū���������Ǥ�3����ä���0����ä��ꤷ�ư㤦��̤ˤʤ뤳�Ȥ�¿���פȤ���ǧ���ʤ�ʤ��Ǥ��礦�����������(2)�Ͽ��ؤǤ�и�Ū���������Ǥ�Ǥ���̿��Ȥ��������Τ��Ȥʤ�Ǥ�����
�Ǥ�������äǤ�(2)�ߤ����ʸ����ޤ路��褯���ˤ���褦��...��
����ʴ����ǡ�

��ˤ�äư�����������³���Ǥ����Ȥꤢ����dot����ˤĤ��ư���ͽ�ꡣ������ø����Tips�����Τ⥢��ʤΤǡ�20ǯ���餤�Τ������Ȥ������θ��ʡ��ˤߤ����ʤ�Τ���������Ĥ��Ǥ˥����Ȥ�äƤߤޤ���
���夲��Τϡ�����̿��̴��Ǻ���١������ϡ�1994�ˤǤ��������Ǥ����ֿ���̿��Artificial Life�ˡפȤ����Τϡ����Ȥ��а��������ǿ����ʶ�ε����Ф����Ȥ����褦���äǤϤ���ޤ��ۥ�륹�Ȥ����������ΤȤ�㤦�����Ȥ������ȤϤʤ�ñ�ˡֿ���ǽ���ʤΥ��֥��åȡ����Τ��ȤǤ���
���㤢�ʤ�ǡֿ���̿�פʤ�Ƹ��äƤ���Τ��Ȥ����С����������ϡֿ���ǽ�פȤ�����Υ�������ǰ����ä�����ǤϤʤ����Ȼפ��ޤ���1960ǯ���Ⱦ���餳�λ��夯�餤�ޤǤϿ���ǽ����ˤȤä�Ǧ�Ѥλ�����ä��Τ��Ȥ����Ȥ�ʪ�ˤʤ�ʤ����Ȥ��ڥƥ�Ȥ������������ݤ�������ơ����֤���ϤޤȤ�ʸ��氷������Ƥʤ��ä��äݤ��ΤǤ���
�����������Żҷ������о�ȡ������餯�ϵ��������ؤ俷����������ʵ��楷���ƥ�Υ��쥳��椹��...�ߤ����ʡ�����ȯŸ���顢�������ä�ƻ��������ǿʹ֤λͤ����λ��Ȥߤϴ�ñ������Ǥ��롢�Ȥ��������ߤ������졢����ο���ǽ����ˤ�¿�ۤ�ͽ�����겼���줿�褦�Ǥ��������������ˤ⤽�������岡���ˤ�븦��ο�Ÿ�ˤ�äơ��¤ϲ�������Ĥ�����ɤ����狼��餤��Ķ������ä����Ȥ��狼�äƤ��ޤ����ȡ�����Ǵ��ø��椫����ľ���ޥå���ȶߤ��������Ȥ���������Х����ɤ���ϼ�˾��ȿư�Ȥ��ƤΥХå����Ф��������...�ߤ����ʴ�����
�ǤϤ��ä��������ԤϤ���˽���ä�����Ρֿ���ǽ�פ�1990ǯ��Ρֿ���̿�פǤϲ����Ѥ�ä��ΤǤ��礦�������Τ�äȤ��礭��������ϡ�����̿�Ǥϼ��Ȥ�������ư�ץ��������ʺ����Ԥ�Ϳ������Τ�α�ޤ餺������ȯ��emergence�˸��ݡפˤ�äƼ�����Ф��ơʲ��Ѥ��ơ��ˤ����Ȥ����Τ褦�Ǥ�������ˤ�äƿ���ǽ�Ͽʹ���ǽ���¤ӡ�Ķ���Ƥ�����ǽ���������������餷����
���Ф������1994�ˤˤϡֿ���̿����������ħ�ϡ�����������̵��Ū�������������ʲ���ǽ���Ǥ���ס�p.12�ˤȤ���ޤ��������ƽ���ο���ǽ�ϡ֤��٤Ƥ��μ���ʹ֤�����������������٤Ƥλ��ݤ沽����ɽ�ݼ���ס�p.15�ˤ˴�Ť���ΤǤ��롢�ȡ��Ĥޤ�ֿʹ���ǽ���ʤ������Ȥ�ɽ���Ǥ��Ƥ���ȼ�ǧ���Ƶ��Ҥ������ơ�������ˤ������֤�������Ȥ�����ΤʤΤ������Ǥ���������Ū�ʵ��沽�ȡ���Ѥˤ�äƤ���줿����Ū���������ȯ��������ԥ塼���ˤ�äƷ�����ס�p.15�ˤȤ�����������Ƥ��ޤ���
���Ȥ��кǶ����֤�����ˤʤäƤ������ǽ�Ǥ����С�Google��AlphaGo�Ͽ���̿�˶��������ܤ���ס����ܥåȤ����������뤫�ˤ�1960ǯ���ǥ�ο���ǽ�˶ᤤ¸�ߤȤ�����Ǥ��礦�����Ԥϡ����������פ�����оݤ��ޤ���
>> �ʹ֤�Ķ��������ե����AlphaGo�ˤϡ��ɤΤ褦�ˤ��ƶ����ʤä��Τ�
���ܡ����㤢���ޤ��ϡ��������Ⱦ����Ȱϸ�ΰ㤤�ˤĤ����ä��ޤ��礦����������ϸ뤬����ʤ˶����ʤä��Τϡ�����ԥ塼�����ǡ������鼫ʬ�dzؽ�����ֵ����ؽ��פȤ���ʬ��θ��椬ȯŸ��������ʤ�Ǥ����ɡ����ֺǽ�˾��ä��������ΤȤ��ϡ������ؽ��Ϥ���ʤ��ä���Ǥ�����ά�ˤĤޤꡢ�������Ȥ���������ϡ��ʹ֤������Ҥ��뤳�Ȥ���ǽ���ä�������������ȡ����դ˴Ը����뤳�Ȥ��Ǥ����櫓�Ǥ����Ǥ⡢�����Ϥ���äȤऺ�������ä���Ǥ���͡�
��ƣ�������ؽ���Ƴ����������������ץ������ζ��������ޥ��奢�͡����ʤ��餤�ǻߤޤäƤ�������������ޤ�����͡�
���ܡ�����ϤĤޤꡢ�ʹ֤��־����ξ��ʻؤ����פ��������ץ������ǽ��Ȥ��Ǥ����Ȥ������ȤǤ���͡��Ǥ⡢�����Ȥ������������ڤ뤳�ȤޤǤϤǤ��ʤ��ä��������顢����ʾ嶯���ʤ�ʤ��ä��櫓�Ǥ��������ơ��ϸ�Ϥ�äȤ�䤳������Ǥ������⤽�ⲿ��ɤ��С��ϸ�Ȥ����������ɽ���Ǥ���Τ����ޤä����狼��ʤ��ä���
��ƣ������ϡ��ʹ֤������Ϥ˸³�������Ȥ������ȤǤ����͡�
���ܡ��Ȥ�����ꡢ���դθ³��Ǥ��͡����դäƤ��ä���̵�Ϥʤ�Ǥ��衣��ά���ץ����������Ǥΰ�Ĥϸ��դʤΤǡ����Ҳ�ǽ�Ǥ��뤫�ɤ����Ȥ����Τϡ��ץ������ˤǤ��뤫�ɤ����Ȥ������Ȥ��礭���ؤ���Ǥ��������ơ��������ϵ��Ҳ�ǽ�ǡ������ϥ��ޥ����ǡ��ϸ�Ϥ櫓�狼��ʤ����Ȥ������夬³���Ƥ��ޤ�����
�綶���ʤ�ۤɡ��������ä�������������˰ϸ�ϡ����դǤ��ޤ������ʤ����Ȥ�¿�����⤷��ʤ����ܤ��Ͼ���ͤ˰ϸ����Ȥ��ˤ�����Ƥ��ޤ��������դ���������ʤ��Ȥ�����ü�ޤäƤ��ޤ����顢���줬����Ĥ��Ƥ���ߤ����ˤʤäƤ��ޤ��ʡ��ȡ�
�����ϰ��ѼԤ��դ��ޤ���������Ĺ�����Ѥ����嵭��Ť�̤Ǥϡ�������ˤ�������̤��ɤ��������֤��ʤɤ��餬�ɤΤ��餤ͭ���ʤΤ������夬�ᤤ�Τ������Ǥʤ��Τ�etc...��������Ū��Ƚ�Ǥ�����ˡ�Ҥ����Ǥ�����٤��ä�����Ƥ���Τ��Ȼפ��ޤ�������Ū�ˤ��äơ��ɤΥ������ǽ�Ū�ʾ��Ԥ�Ƚ�Ǥϳμ¤˲�ǽ�Ǥ����Ǥ����餳�����餫�ʺǽ���Ū�ʡἫʬ�����ԤȤʤ���֡ˤ˸����äƾ��֤����ܤ����褦�ȥ������Ȥ���������֤��Ƥ������Ȥˤʤ�ޤ������ΤȤ�Ŭ�ڤʥ��֥������ʤ��Ȥ��Х�����������ˤ�����Ͷ���å��ʤɡ��������̲��������ꤷ�Ĥġ����������˸�����ʤ����ư���ʤ���Фʤ�ޤ���
�Ĥޤ�����ˤ����Ƽ��٤�ɬ����ά�������Ǥ���С����Υ�����ϴ���������Ū�˵��ҤǤ������Ȥˤʤꡢ������ά��Ȥ����Τޤޥץ�����ಽ�����1960ǯ�巿����ǽ�С��������夬��ΤǤ����ǡ��������䥪������ޥ�Хĥ�����ǤϿʹ֤Ρ���Ѥˤ�äƤ���줿����Ū�����פ�ȤäƤ��������ץ�������������뤳�Ȥϲ�ǽ���ä��櫓�Ǥ����顢������ˡ�Ǵ����˿ʹ֤ˤ�ä����칶ά���줿�Ȥ������ȤǤ⤢��ޤ���
������������ϸ�Ǥϰ�ä������ˤ��ä��餷�����嵭�β��������ս�ǤϤ�����⤽��ˤĤ��Ƹ��ڤ��Ƥ��ޤ���������Ǥ⸽�ߤǤ��̤���ˡ�ǺǶ���٥�οʹ֤��Ǥ��餫����Τ�����ޤ���������ɡʥ������ʤɤȤϰ�äơˤ��Τ��ȤϾ�����ϸ�Ȥ��������ब�ʹ֤����Ƥ�������Ū�����줿���Ȥ������Ȥ϶��餯��̣���Ƥ��ޤ���
�����1994�ˤ�����Ѥ��ޤ��������ϰ��ѼԤ��Ĥ��ޤ�����
���ޤΥ���ԥ塼���ˡ������Ȥ��Ƥ��Ƹ��դ�����������Ǥ��ʤ����Ȥ�餻�뤳�ȤϤޤ��Ǥ��ʤ������դ������Ǥ��ʤ�ǽ�Ϥ�������̿�Ȥ�������Ū�ʼ��ʤdz����Ǥ���Ȥ���С����Ф餷�����ȤǤ��롣����̿�Ͽ���ǽ�ιԤ��ͤޤ���dz����������μ���Υ���ԥ塼���Ϥ�ä���Ū�ˤʤ������������Ϥ�����̴���������ζ�����������ϡ�����줬������Ū����פ��������ͤФʤ�ʤ����ȤǤ�������p.114��
�Ĥޤ���AlphaGo������̿�Ǥ���Ȥ�����������̤�Ǥ���ʤ顢�Ǥ����������ʹ֤ˤ�������ã�Ǥ��ʤ��������θ����Ƥ��뤬��������ؤΡ�����Ū����פ���������Ƥ��ޤäƤ���Ȥ������ȤʤΤǤ��礦���Ƕ��ΰϸ����ǽ����Ф��Ϥ�����ΤΡ��ʹ֤ˤϤ��줬�ɤ�����ǽ�ϤǤ��뤫����ϤǤ��ʤ��ʡ�����Ū�������ҤǤ��ʤ��ˤȤ������Ȥ��ȡ����줬�������ˤ���褦�ʡֶ�����������פ��ȹͤ����ޤ���
������������������ʥ�٥�������������Ȥ��Ƥ���Ȥ��������̾Ρ�����ܤ���פϤɤ�ʴ����ʤ�Ǥ��礦����
�Ȥ����ǡ���������Ϥɤ����ƺ��Υ��������³����Τ����������������������Ȥ⡢¾�Τɤβ��ܤȤ���ؤ������ʤ��Τϼ��Τλ��¡�������֤��줬����Ϥʤ�Ǥ��פȤ�����ĥ�����äƤ⤤�����ɡ���������ϤʤΤ�������ơ����ä���������٤��ʤ�ʤ����Ȼפ�졣��24 Dec 2015��
�ץ��������ȥǥ��쥯�����Ǥ����ʪ��tweet����Ѥ��ޤ����������ϰ��ѼԤˤ��ޤ����ʤˤ����λ����˶�����äƤ�褦�Ǥ���...��
>> ���浪�Ҷ�����ͽ�������ܥåȤǼ��Ȥ���Τϡֶ�Ԥ�����פ���Ⱦ��ľ����
��2015ǯ������ܤ���ϥ�����������Ԥ�8�������������40���ͤι3ǯ���Ȱ��˿ʸ��ޡ����ϻ�������5���ʹ�פ�����ʿ�������礭�����ä���
���ä˿���IA������IIB��������B�Ǥϡ�����ʿ�Ѥ�30�������ޤ��������ޤ�������й�������Фޤ�����������ʸ̮�ʤ���Фʤ�ʤ�����Ѹ�ϸ������Ǥ��͡��ޤ�ʪ��������ʿ�Ѥ��ޤ������褯���ؤ��Ǥ����ʪ����Ǥ���ȸ����뤬ξ�ԤϤޤä����ۤʤ��ΤǤ���
���϶����ܤ����͡�����Ū�ˤ�200��������90�����к���45.1�ߤ����Ǥ��ʢ������ˡ���������ϥ��Ĥ����Ǥ��ʡʾС��ˡ��ϻ�γ���ʿ������105.4������¾���ʤȰ�äơ�Ⱦʬ��Ķ���Ƥ���Τ⤢�ä�;����Ω�ĤΤ��ȡ�
����Ū�ˤ��Υץ��������Ȥοͤ����������äƤ���Τ��������Τ�ʤ��ΤǤ��������ʤ��Ȥ���ˤĤ��Ƥ����Ρ���Ѥˤ�äƤ���줿����Ū�����פ���ˤ˿�������ˡ�Ǥ�ͭ������ά��ȯ���Ǥ��Ƥ��ʤ��ȹͤ����ɤ��Ǥ��礦���Ĥޤ���첽������ʤ��ᤦ�ޤ��ԤäƤ��ʤ��櫓�Ǥ���
�ǡ�AlphaGo���ä��͡��Ȥδ֤ˤ����ܼ�Ū�ʺ��ۤϡ���ά�оݤ˸����äơ֤��ä���������٤����ʡ���첽�����������ᤷ�Ƥ������Ǥ�������Ǥϰϸ륽�եȤ����ˤ�������Ȥ��äƥ������Τ褦����ά������Ū�˵��ҤǤ���褦�롼����ѹ����ƤϤɤ������ȸ��äƤ���Τ�Ʊ���Ǥ����ʻ��͡������Ȥˡ�����ܤ����¦��AlphaGo�ζ������礤�˹������ֿ��سؽ��פ椹����ͤ��ʤ���Τ����Ǥ��Ƥ��ޤ������ο���ǽ���椬���ܤ�쵤��ȴ����ä���ͳ��
���ơ������������Ȥȴط�����褦��̵���褦���äǤ����ʢ�����1960ǯ�巿����ǽ���������Ȥϡ���ɡ�����Ū�˸��䤹�����ƤΤߤҤ��ơ����������Ȥ���פȤ�������ž�ݤ��ˤ��ä��Τ��Ȼפ��ޤ�������Ū�Ǥ��뤳�Ȥ����ˤ�����äơ����줬���¤�������Ф���̵�Ϥ��ä��긫���㤤�η�̤�Ф��Ƥ��ޤ����Ȥϰդ˲𤵤ʤ�������ɤ��������¤���������˹�碌���ȶ��ۤ��롣���Τ��Ȥ�����ʿʹ���ǽ������Ѥˤ�äơ����߽Ф�������ǽ��ְ���������Ū��ν����θ����פˤ��Ƥ��ޤ��ΤǤ��礦��
����ǽ�κ����Ԥ���ǽ������äƤ��ޤäƸ��������ν�������ʥ���Ĥ��ʤ�����ո����������Ȥ����Τϡ������Ϻ�ʤɤ�������Ƥ����ֿ�������Ǥ�Ƴ������Ū�ʿ���ǽ�����ȽŤʤäƤߤ��ޤ���������������ǽ���Ȥ����ΤϤ����οʹ���ǽ�Τ�������ȿ�Ǥʤ櫓�Ǥ����顢����Ͽ���ǽ����ڤ�����Ū�˼Ҳ�ˤ⤿�餹����Ȥ������ϡ��Τ��餢��ʹ���ǽ�����ꡢ�Ȥ����������οͳʤ��Ŀʹ֤��Ҳ�˵ڤܤ����������Ū����������Τ��ä���ʤ����ȡ��ܲ�����ץ饳��ץ龧����Ǯ����Ư���͡��ˤ�äƻ䤿���μҲ�ϰ۾�˵�������Ψ�ʤ�Τˤ�����������ˤʤäƤ��äƤ��ޤ����...��
����̿Ū�ʿ���ǽ��1960ǯ�巿����ǽ�δ֤ˤ��뺹�ۤˤĤ��Ƥϸ����ǥ�Ȥδ�Ϣ�Ǥ⤫�ʤ�����������ȤϤ���ΤǤ������������Ĺ���ʤ�ΤǤ����ǤϺ��������Ĥġ������1994�ˤ��餤���Ĥ��ȥԥå���ȴ���Ф��Ƹ�äƤߤޤ���
�ޤ��ϡְ���Ū���르�ꥺ���genetic algorithm�ˡפˤĤ��ơ��ǡ������1994�ˤ����Ƥ����Ҳ𤷤Ĥġ��Ȥ������ϳ�ȼ�ͳ�ˤ�����ǻפä����ȤȤ��������������ȤˤĤ��ƽƤ����ޤ���
��̿����������ħ�ΰ�Ĥϡ����οʲ�����ǽ�ʥ����ƥ�Ȥ������ȤʤΤ����ʲ��ϻ���Ū��ȯŸ�β����ǡ������ҷ������¸��ͭ���ʹ�¤��������ˤ�äƽ缡��������������ͭ������ʬ��¤���༡��礹�뤳�Ȥǡ����Ķ��Ȥ����Ѳ���Ŭ��������Τؤ�ȯŸ����������ȯŸ�������ʤ���ʲ��ϡ����ĤȤ��Ƥλ���ȯŸ������Ŭ�������ܼ��Ǥ��롣��p.27��
Ϳ�����Ķ���Ŭ�����ơֿʲ��פ���褦�˿���̿���߷סʡ��ˤ���Ȥ����äΤ褦�Ǥ������餫�λ����ǴĶ���Ŭ�����ʤ���Фʤ�ʤ����Ĥ����ꡢ���ι������ǤǤ���ơָ��Ρ�individual�ˡפˤϡְ����ҷ���genotype�ˡפ�ɳ�Ť����롣���沽���줿����Ǥ���ְ����ҷ��פ��Ф��Ƹ��Τ��Τ�Τϡ�ɽ������phenotype�ˡפȤ�ƤФ��ߤ�����
�ǽ�ΰ����ҷ��ϸ��Τ�ͭ���ͤ沽���뤳�ȤǺ����櫓�Ǥ��������θ�ϰ����ҷ����餽��ɽ�����Ȥ��Ƹ��Τ����Ф���Ƥ����ޤ��������Ƹ��Ρ�ɽ�����餫�λ��Ȥߤˤ�ä�ɾ���������η�̤˴�Ť��Ƽ�����˻Ĥ������ҷ������̡��ǡ������������Ф줿�����ҷ�����˰���γ�Ψ���ʸ������Ѱۡ��������ʣ�ʤɤΡ��Ѳ������Ȥ����������Ȥ߹���ǡ�������ΰ����ҷ�����ꤹ��Ȥ��������֤�����ǴĶ�Ŭ���˴ؤ��ơ�ͭ������ʬ��¤�פ��ʤ��building block������ҷ����������Ƥ������ȡ����ȤȤ��ƤϤ����������ȤߤΤ褦�Ǥ���
�����1994�ˤǤϡ�����ס�Ȭ�ܥ��إ��ܡס֥ͥ��ߤ���館��ǭ�סֿ�ʪϢ���פʤɤ��㤬�ФƤ��ޤ������������С����⤽�⤳���ܤ�䤬�Τä����ä����Ȥʤä��Τϡʤ��֤ˡط���������٤ǡ�Ȭ�ܥ��إ��ܡסʢ����ȡ�Khepera�ˤ˴ؤ��륳�����ɤ�����Ȥ��ä��褦�ʡ�
�Ǥ⡢�����ϴ����Ʋ����̤ζ�����ǹͤ��Ƥߤޤ���
���Ȥ��С�������������١ʹ������ס�2015�ˤ�ñ��٥���ʬ���ˤĤ��ƽҤ٤���ʬ�˽ФƤ������ǥ��Υ����������ʤϤɤ��Ǥ��礦�������ξ��������ϡֿ����֡��ġ����ˡסֳޤη��ʴݡ��ͳѡˡס�����Ĺ����Ĺ����û���ˡס־��ʼ��ڡ����̡ˡס��ǡʤ��롿�ʤ��ˡפȤ���Ƥ��ޤ���������ϰ����ҷ��ʡ�������«�ˤ�����Ȥäƥ��Υ���ɽ���������Ȥ���������Ǥ���
������2015�ˤγ����ս�Ǥϡ�8�ĤΥ��Υ��եǡ����˻Ȥ������������ǰʳ�������«����Ӥǡ������ҷ������פ��ʤ�̤�ΤΥ��Υ��ˤĤ����Ǥ�̵ͭ��Ƚ�̤����Ƥ��ޤ���������Ū���르�ꥺ��λ���Ȥ��ƻȤ��ʤ顢���륭�Υ����ݶȼԤ����ơ��ǽ�Ϥ��ζ��եǡ����ˤĤ��ä����Υ����Ĥ�Ʊ�ͤΰ����ҷ�����ä����Υ�����ݤ���Ȭɴ���˲�����������ʹߤκ��ݷײ��Ȭɴ�����ġ��Υ��Υ����㤤��ä��Ȥ������ʤ˱������Ѳ����Ƥ������Ȥ����褦�ʤ�Τ��ͤ����ޤ���������֤��Ƥ����ȡ����Υ����Ĥ��ֿʲ��סʡ��ˤ��뤳�Ȥǡ������פ�����ʡ��ɾ��������˰����ҷ���ȯ���˷Ҥ��äƤ������ȴ��ԤǤ���ΤǤϤʤ��Ǥ��礦�����Ķ���ֲ٤�����פȹͤ����ʲ��ˤ�äƤ����Ŭ�����������ҷ��Ρֲ�פȤߤʤ����Ȥ�Ǥ��ޤ���
���ΤȤ����ܤ��٤����ϡ�Ȭɴ���Υ��Υ���襢�르�ꥺ�ब����Ū�ˤ�����Ǥ��ʤ��ޤޤǤ�Ŭ�ڤʺ��ݷײ����ꤷ�Ƥ������Ȥϲ�ǽ�Ȥ����Ȥ����Ǥ����Ȥ����������⤽�����δ����㤤��äƤ����ݾڤ⤢��ޤ���ɾ����ऽ�Τ�Τ�����ʶ�ȯŪ���װ����ߤǡ���ư���Ƥ��äƤ���Τ��⤷��ʤ���
�����ʤäƤ���ȡ����Ȥ��Ф�������ǡֺ�Ŭ�ʡ��פȻפ�������ҷ������Ĥ��ä�����Ȥ��äơ��������粽�Τ���ˡ����ΰ����ҷ�������������ݤ��Ƥ������Ȥ�����ά���ʽ��Ĥ�ɾ��ʿ���ͤ�Ǥ�������⤯�ݤ�³�������Ȥ�����ɸ�ˤȤäơ����Ѵ������Ȥ狼��ޤ����¼Ҳ�Ǥ������Ƚ��桪�פߤ����ʤ��Ȥ���äư��Ū�ˤ��礭�����פ��ĤĤ⡢�Ծ�Υˡ������Ѳ������Ŭ����ǽ�Ȥʤäƾ���...�Ȥ������Ȥ������褦�ʡ�
dot�����Ȥä����쥳��ΤȤ����ޤǤ��ɤ�Ĥ��ä�...���ޤ�����ȯ�פ���ʤ��ȥ���ʤ�����ɡ�����˴�Ϣ���ơ��������פˤ���ڤ��ʤ��Ȥ����ʤ������Ȥ����Τ�����ʡ��ˤ�����Ǥ褦�䤯�˥塼���ͥåȤ��ä����äơ�����Ǥ�ä�dot����ν��֡�

�����Ͼ���ճ�Ψ�˸��ڤ��ޤ�����������Ψ�쥳�줷�ƻ����Ψ��夲���겼�����ꤹ����ȤߤʤˤĤ��Ƥιͻ��Ǥ���
�褯������������ܡʡ��ˤʤ��ȡ����Τ��ȡ�ñ��٥���ʬ����naive Bayes classifier�ˡפ��äؤȰܹԤ���Τ����֤ߤ�������Ψ�ѿ��ˤĤ��Ƥξ�����Ȥˤ���̤�Τλ���ʡ��ˤε�°��ʡ��ˤ����Ǥ����ˡ�Τ�����äȤ�ʰפʤ�Ρ��Ȥ������ʤ�ͤ���ȶˤ��������ή��Ȼפ��ޤ���
���Ȥ��С�����ʤ�狼�롪�٥������׳��١�Ͱ���ɹ���Ͱ��������2012�ˤǤ⤽��ʽ�Ǥ��������ʤߤ˽��Ǥˤ��ä��Ѥʥߥ��ʤ��Ȥ�����Ƭp.8�Ǥ����ʤ�٥����������������ְ�äƤ����ꡢp.40��3/52=1/4�Ȥ��������ʬ�����ä���...�ˤ���8���Ǥ�ľ�äƤޤ����������Ȥʤꡣ
��ǯ��������ؼ��Ȥζ��ʽ�Ǥ����������������١ʹ������ס�2015�ˤ���4�ϡ�ʬ������Ȥ��Ƥμ�����������פǤ���ڤ�����ޤ�������1����3�Ϥ�Ƴ���Ȥ���������ߤ����ʤ�Τ��ä��Τǡ�����Ū���ä��Ϥޤäƿ�����˽ФƤ����ͥ��ȸ�����ΤǤϤʤ����ȡ��ǽ�ξ��ܥ��Ȥ�������ܥ��Ȥ��������ʤ�Ȥ���������ʴ�����
�ǡ���®�Ȥ꤫���ꤿ���ΤǤ���������ˤϰʲ��Τ褦�ʿޤ����ˤ˽���Ȥ������ݤ����������äȤ��ʤ���褦�ʥ��쥳���ɬ�פˤʤäƤ��ޤ����Ȥ�������̵���ȥ�å���ɤ���
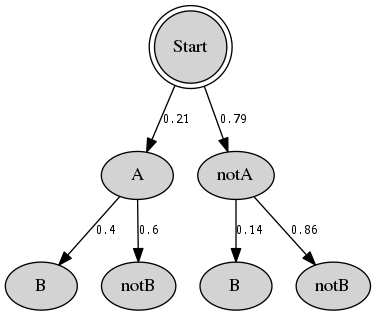
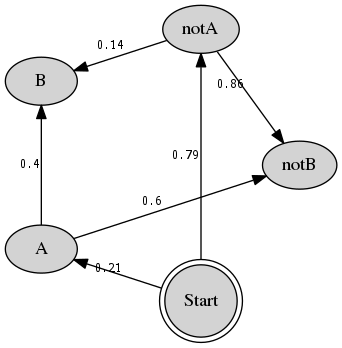
������Emacs��org-mode���äƤߤ뤳�Ȥˤ��ޤ��������ε�ǽ�äƥ������塼������˻Ȥ���Τ��ȻפäƤ��ΤǤ��������������ʤ��ä���Ǥ��͡��ȡ��������Ĥ�������ǽ�ˤĤ��Ƹ��ڤ��Ƥߤ褦�Ȼפ��ޤ���
Emacs�ˤ�org-mode�Ȥ����Τ�����餷�����Ȥ����ΤϺǶ�ʢ������Τ�ޤ������ɤ�����ΤΡ֥����ȥ饤��⡼�ɡפ�ȯŸ�����ʡ���ʪ���ѡ���������Τäݤ������ʤߤ�org-mode�����븽�ߤǤ���M-x outline-mode�Ȥ���mode line��Outline��ɽ������ޤ�����Ƭ�������ꥹ����Ⱦ�Ѷ���Τ��Ȥ˽�ʸ����Ͽ����Ѥ�äơָ��Ф���ǧ�������ΤǤ��Υ⡼�ɤε�ǽ�������Ƥ�äݤ���ñ���org-mode���֤�����äƤ��ޤä��櫓�ǤϤʤ��Ȥ������Ȥ��ȡ�
outline-mode�Ǥϸ��Ф��Υ�٥���硢�桢�����ˤ�ʸ�Ϥ��ز����뤳�Ȥ���ǽ�Ǥ��ꡢ�����ơʤ��֤ˤ��줷���Ǥ��ޤ���org-mode�ǤϤ�ä�¿�̤���ʣ���ʤ��Ȥ��Ǥ���褦�Ǥ������Ȥ��С�����������ǽ��Ϣ�Ȥ����������塼������ġ���Ȥ����̤Ȥ���
TODO���Ȥ�DONE�Ȥ��ä��ڤ��ؤ���ǽ��ɽ�������ѤǤ��롢��ɽ��ʳ��ع�¤�Τ���˽���ǽ�ΤĤ��������å��ꥹ�Ȥ��ñ�ˤĤ����������ͽ����������ʤ��鸫�̤��褯���ؤ��İ�ϳ�ʤ��������Ƥ�������Ȥߤ����������Ѱդ���Ƥ���褦�Ǥ�����������ȥ������ޥ��������ꡣ��ˤ����äȽޤ��������ǽ��org-mode���Τä����ä����Ϥ������ˤĤ��Ƥδؿ�����Ǥ�����
���Τ���������Ȥ������̤����̤Ǥ�Ϥʵ�ǽ��ͭ���Ƥ���餷�����Ȥ˵��Ť��ޤ������ޤ��������ΤǤ�������ĤΥե������˥�����ץȤ�Ƥ��ξ�Ǽ¹ԡ�C-c C-c�ˡ���̤��̸���Ǥޤ����Ѥ���...�Ȥ����褦�ʻȤ������Ǥ���ΤǤ����䤬��ǧ���Ƥߤ������Ǥ�C++��Ruby��Emacs Lisp��Perl��Shell Script�ʤɤ��Ȥ��ޤ������ޤ�TeX�νǵ��Ҥ��������ξ�Dz����Ȥ���ɽ�������ꡢR����ǥ���դ��������ʤɤȤ��ä����Ȥ�Ǥ��ޤ���������Ǥ����ȡ֥����������ɤȼ¹Է�̤�Ʊ��ե�����ˤޤȤ���ǽ�Ȥ������Ȥ��ȡ�
�嵭��¾�ˤ⤳���������ѤǤ���ʹ����Ρ��˷�������Ϥ�������褦�Ǥ���������������Τ����dot�����DOT���졩�ˤ�����ޤ�������㼨�����ޤϤ����Ȥä������ޤ������繽¤ʸˡ�ΤȤ����Ǹ��ڤ��������ȥޥȥ٥����ͥåȥ������ƥ�����¤�ߤ����˥Ρ��ɤ�����Ƿ�����Ρ����ܿޡˤ�������ʤ������ع�¤���ĥ��Τˤ⤳�������ġ��뤬ɬ�פˤʤ�ޤ���
���ʤߤ�¿�����Ʊ�����Ѥ��Ǥξ��֤�org-mode�����Ǥϥ����org-babel�ʤ����ꡩ�ˤ�ɬ�פˤʤ�ޤ���dot����λ��Ѥ˺ݤ��ƤϳΤ��ˡ�org-babel-do-load-languages�ױ�����Emacs����ե�����˽��ߤޤ��������Τ�����Υ��쥳��ˤĤ��Ƥ�org-mode�ΥС�������鲿���Ƿ빽��äƤ���餷����������䤳�������Ȥ⤢��褦�Ǥ����Ȥꤢ����Ŭ���˥����äƤʤ�Ȥ�ư�����Ƥ�������ʤΤǤ���ޤ�뤳�ȤϤʤ��ΤǤ����ɡ�
�ȡ������櫓�Ǿܤ����ʡ����äϷ�ɼ���ʹߤȤ������Ȥ�...��
Copyright(c)2006-2016 ccoe@mac.com All rights reserved.