
1119 1027 0928 0830 0727 0628 0531 0503

前回とその前では「関数(写像)」についてアレコレ書いてきました。どうやら「関数」には「対応関係」と「従属変数」の二通りの用法があって(関係が数式で表せたりすると特に)一般には後者の意味が普通らしい云々。
さて、すったもんだしながらも「論理」「集合」「関数」が同様の何か(?)であるらしいことはなんとなくつかめてきたような気がします。文系ちゃん的ゆるふわ理解ですけろ(笑?)。今回はそれに「条件付確率」を加えようという魂胆です。
そういうわけで早速まずは「論理の箱庭」召還。
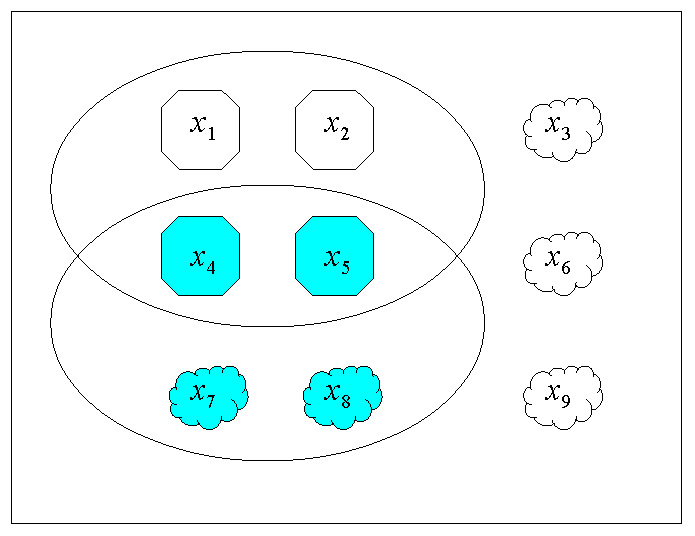
すべてのxについて「八角形である」という性質を持つ要素の集合P(x)と「色つきである」という性質のQ(x)をあらわす円が描かれています。このときの集合P(x)は述語論理の命題文「xはPである」も意味していました。
関数Pについてはどうでしょうか。
P:X→Y
X={1,2,3,4,5,6,7,8,9}
Y={true,false}
G={(1,ture),(2,true),(3,false),(4,true),(5,true),(6,false),(7,false),(8,false),(9,false)}
Xの要素はx_1,x_2,...ですが面倒なので(←!)数字だけにしました。
集合P(x)は「P(x) is true」の意味ですが、同時に「notP(x):=P(x) is false」も明らかにしているということから、universe=domainの要素を二種類(trueとfalse)に仕分けする役割をしていたことがわかります。ですから、これは要素xが属する集合Xから{true,false}という二つの要素だけを持った集合Yへの2項関係であり、right-uniqueとleft-totalも満たしているので関数だと捉えることができます。xに対応したcodomain集合の要素はP(x)なので(XとYの直積集合のうち)グラフGは(x,P(x))が妥当である組み合わせの集合です。
集合を視覚化するときベン図を用いるのが普通で、また大抵の場合、複数の集合が同時に書き込まれているのを目にします。このとき集合を表す円とその重なり方にだけ目がいってしまって、各集合が背景の四角い枠であるuniverse=domainをそれぞれに「二分している」という部分への意識が希薄になってしまっていた気がします(何かと数学が不自由な俺ちゃんだけかもしれませんけろけろ:汗?)。
そこで「xを二分する」という感覚を強く打ち出すために(要素xの位置は適宜動かしつつ)直線で表してみます。最初に提示した「論理の箱庭」は以下のような図に書き換えられます。
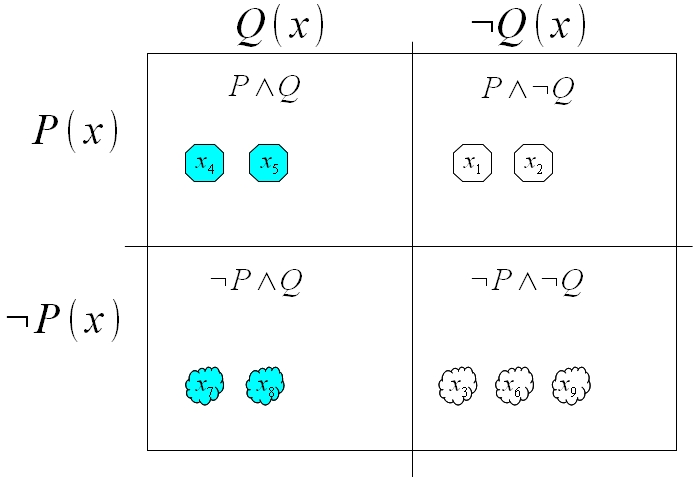
P(x)やQ(x)がtrueであるときを「P(x)」「Q(x)」、falseであるときは「notP(x)」「notQ(x)」として、universe=domainのニ分割を二回で四分割しました。上下でみると「かたち」で、左右でみると「いろ」を基準として分かれていることがわかります。
さて、これから「確率」を扱うに際して四分割された領域というか集合のうち三つが同じ要素数では何かとうまくありません。また色々と都合の悪いことはそれだけではないので、基本的な部分はそのままで使い勝手が良くなるようにアレコレ変えてみようと思います。
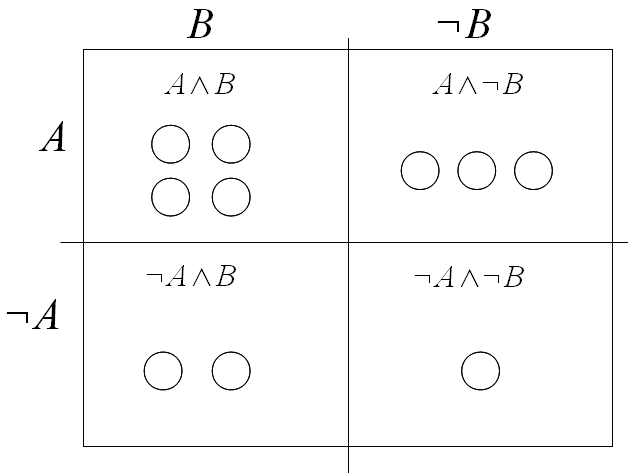
「P(x)」を「A」に、「Q(x)」を「B」に変えました。universe=domainの要素xをひとつ増やして10個にし、四分割された各集合の要素数を全部異なるものにしました。八角形や色つきだったりした要素をすべて同じ白丸で表したところも変更点です。
これらは、確率の問題を扱うときに「集合の要素がどのようなものか」はあまり重要ではない(たぶんそういうことはtopologyで扱うと思われマッスル)のと、確率関数(?)的なものに「P」という字を使いたかったからです。
で、関数Pにしちゃうとやっぱりなんかアレなんで関数Prにしときます(もちろんProbabilityのPrです)。これは条件付確率を求める関数です。なお「基数」というのは要素の個数みたいなもので、無限集合なんかのときは「濃度」と区別するようですが、英語ではどっちもcardinalityというらしいです。集合名(?)を絶対値のときみたいに両側を縦棒(←!)で挟んで表す模様。ordinalに対してcardinalということかと
Pr(M|N)とは?
(1)条件NのときのMの確率、という意味である。
(2) 集合「N」の基数と、集合「MかつN」の基数の比を求める(「MかつN」の基数/「N」の基数)。
(3)「N」が省略された場合には、全体集合「U」の基数と、「MかつU」つまり「M」の基数との比を求める(「M」の基数/「U」の基数)。
改訂版「論理の箱庭」で計算してみます。
Pr(B|A)=|(A and B)|/|A|=4/7
Pr(A|B)=|(A and B)|/|B|=4/6
このとき以下のことがいえます。
Pr(A and B)=|(A and B)|/|U|=4/10
Pr(A)=|A|/|U|=7/10
Pr(B)=|B|/|U|=6/10
Pr(A and B)/Pr(A)=(4/10)/(7/10)=4/7
Pr(A and B)/Pr(B)=(4/10)/(6/10)=4/6
たぶん(←!)いつでもこうだと言えるんで、最初の計算に使った式を以下のように書き換えることができます。(というか、ぶっちゃけ「AかつB」の確率って「事象A(or B)が起こってしまった状態の後で事象B(or A)が起きる確率」に「事象A(or B)が起きる確率」をかけたものになる、っていうのはゴチャゴチャ考えるまでもない話のような...(汗)。もとが「論理の箱庭」だったのでアレな感じですけろ。いずれにせよ関係式をちょいちょい弄れば以下の二式になりますしおすし)
Pr(B|A)=Pr(A and B)/Pr(A)
Pr(A|B)=Pr(A and B)/Pr(B)
で、この二つの式はPr(A and B)が共通ですので以下のように書けます。
Pr(B|A)=Pr(A|B)Pr(B)/Pr(A)
Pr(A|B)=Pr(B|A)Pr(A)/Pr(B)
「A(or B)という条件のもとでのB(or A)の確率」という従属変数は、独立変数「Aの確率」「Bの確率」および「B(or A)という条件のもとでのA(or B)の確率」によって記述できる、ということがわかります。なんつかよくわからんですけど、この式で表されるようなことを「ベイズ定理(Bayes' theorem)」というらしいのです。
えーと、「ベイズ」というのは忌み名ですんで(←!)あんまり触れずにいきたいと思います。上でアレコレした結果をもとにもう一段階「論理の箱庭」を改造すると以下のような感じかと。

要素や基数は関係なくなって確率だけです。箱庭と呼ぶには一般化されすぎな気もしますが(笑?)。あとこれに関する諸式(?)はこんな感じで(あ、ベイズ定理の式は普通は下に示したのとA、B逆に書きますね...)。

さて、問題はこっからなんですよね。これをどうするかっていう。
何か例題(?)をやってみましょう。『異端の統計学ベイズ』(2013、シャロン・バーチュ・マグレイン)のpp.455-459にある「補遺b 乳房X線撮影と乳がんにベイズの法則を適用する」からアレコレ。
求めたい従属変数は「マンモグラム(=乳房X線撮影)検査の結果が陽性である」という条件のもとでの「40代女性が乳癌である確率」だそうです。つまりPr(癌|マンモ陽性)を求めたいと。「論理の箱庭JK(Jyoken-tsuki-Kakuritu:笑?)」を参照すると以下の通りになるのがわかります。
Pr(G|M)=Pr(M|G)Pr(G)/Pr(M)
「40代女性が乳癌である」is trueをG、「マンモの結果が陽性である」is trueをMとして立式してます。
Pr(M|G)は乳癌の人がマンモグラム検査で陽性になる確率で、調査により4/5(80パーセント)とわかっているのだとか(ちなmammogramやmammographは乳房X線写真のことでmammographyが乳房X線撮影(法)なんだとか)。Pr(G)は乳癌の確率ですが(アメリカの?)40代女性では1/250(0.4パーセント)であると(一般的には「低い確率」と捉えるようですが私は思ってたよりずっと多いと感じました...単なる感想ですが...)されます。残りのPr(M)はマンモグラムで陽性になる確率で257/2500(10パーセントちょい)だそう(蛇足ですが257は55番目の素数にして3番目のフェルマー素数...ほんとどーでもいーけろ...)です。これら事前に分かっていた確率の数値を独立変数にぶっこみますと計算ができます。
Pr(G|M)=(4/5)(1/250)/(257/2500)=8/257=0.0311284...
なんとマンモグラム検査の結果が陽性という「癌かもしれません」通知をもらった人のなかで本当に癌である人は3パーセント程度だという計算結果です。Pr(M|G)=4/5よりマンモグラム検査の信頼度(?)が80パーセントだと思っていた(から80パーセントの確率で癌なのかと思ってショックを受けてた)のに、実際には97パーセントがハズレだと。なんじゃそりゃと。ととと。
統計学をはじめたばかりの学生や医師の多くが、これを知ってびっくりする。なぜならマンモグラムはそれなりに正確なスクリーニング検査であるからだ。実際この検査を行うと、その時点で乳がんになっている四〇歳の女性の約八割を把握することができて、病気でない女性の約一割しか陽性にならない。(p.455)
引用は上記マグレイン(2013)から。
アメリカ政府の特別チームは「ベイズの法則」から計算した結果をもとに「40代女性はマンモグラム検査を受けない方がよい」的なことを言ったところ(上で引用したような認識を持つ)世間を激怒させてしまったのだとか。うーん...。
このように、ベイズを使うと、乳がんのスクリーニング技術を向上させて偽陽性の数を減らすことがいかに重要かがくっきりと浮かび上がる。ちなみにもう一つ、マンモグラム検査の技術を向上させる必要があるということを示唆する事実がある。この検査で陰性が出たためにがんを見過ごす例が、がん患者五人につき一人の割合で起きているのだ。(p.458)
そ、そうなのか。ということでまず「もしもPr(M|G)が100パーセントだったら...」とかをやってみます。乳癌患者に検査を行うと100パーセント陽性が出る検査だとしたらどうか?みたいな。
Pr(G)はそのまま1/250で、Pr(M)も257/2500に固定しておきつつPr(M|G)だけ4/5から5/5=1に...っと。Pr(G|M)=Pr(M|G)Pr(G)/Pr(M)=(1/250)/(257/2500)=10/257=0.0389105...4パーセント弱にアップ!...ってアレレ?
あー、なるほど、Pr(M|G)が100パーセントだから見逃しはなくなったとしても、それによる精度の改善は(もともとそれなりだったので)さほど見込めないと。乳癌の発生率Pr(G)が1/250つまり0.04パーセントしかないのに、マンモ陽性率Pr(M)が257/2500=約10パーセントと、ここが大きく乖離してたのが主因だったんですね。だから偽陽性率1-(Pr(G)/Pr(M))は依然として高く精度は低いままになる、と。
つまりPr(M)を固定したままPr(G)が上昇するとか、Pr(G)は固定したままPr(M)を下げるかして、マンモ陽性率と癌発生率の値が近くなれば、Pr(G)/Pr(M)が1に近づく。そうするとベイズ定理の関係式よりPr(M|G)の値がPr(G|M)にそのまま反映されるようになる、で、精度があがる、ということか。
なるー...しかし、so what感は否めない...(笑?)。
ベイズ定理についてもうちょっと粘着してみます。
おい誰だよキットソンのバッグ持ってる女はヤレるっつってた奴 出てこいよ ヤレるヤレない以前に大体茶髪のビッチ臭いやつはみんな持ってるじゃねぇか 片っ端から行けってかオイ
上で引用したのはtwitterで見かけた発言です。えー(苦笑?)倫理的なことはさておき、これは条件付確率を考えるときにちと面白いかな、と。
真面目で深刻な医療問題とナンパの話ですんでアレなんですが、実は上で見てきたマンモグラムの話と共通する構造(?)が見てとれます。まずPr(G)つまり「40代女性が乳癌である」確率にあたるのが「ヤレる女である」確率(=Pr(A)としときます:汗)です。
そしてtwitterの発言者は「キットソンのバッグを持っている」(=Bである)という情報を利用して「ヤレる女」に出会う確率(=Pr(A|B))を上げようと企んでいたわけですが、これはアメリカ医療当局が「マンモグラム検査の結果が陽性である」(=M)ことを利用して「乳癌である40代女性」に出会う確率=Pr(G|M)をできるだけ高くしたいという目的を持っていたことと似ています。
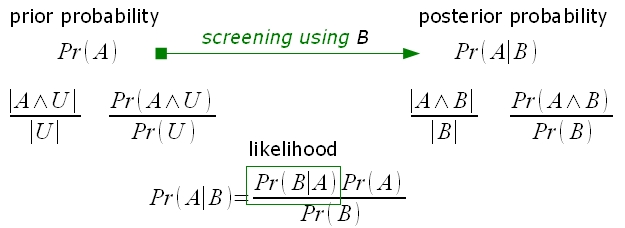
どちらのケースも上図のような仕組み(?)ではないかと。「U」は前述の通り「全体集合」つまりuniverse=domainのことです。Uに対するAの比から、Uの部分集合であるBにおけるAの比率というように、範囲を狭めることでAの含有率を上げようとしています。
こう捉えなおすと、Pr(G)=0.4パーセントだったものをPr(G|M)=約3.1パーセントまで、つまり約7.8倍も上昇させたのですから、マンモグラム検査は決して無駄とはいえない気がしてきました。「受けない方がよい」は言いすぎかと。
たとえば「論理の箱庭JK基数版」での計算結果と比較してみます。

Pr(A)=7/10=0.7に対してPr(A|B)=(4/10)/(6/10)=2/3=約0.67ですから「Bである」を利用した結果下がりました。まあ、下降させるのが目的だったら効果があったことにはなるんですけど(犯罪に遭遇する率とか事故率とか、下げた方が良い確率はありますからね...:汗)。
さて、この図を利用しつつ、四分割した各集合の基数がどういう分布をしているときPr(A|B)が急上昇するのかを考えます。アメリカ医療当局にもナンパ師にも必要なアレだと思いますんで(笑?)。
単純な話、「AかつB」の部分にAの要素が全部固まってればいいんですよね、まずは。そうすると取りこぼして減る分(=「AかつnotB」の分)が無くなるので、分子の基数は分母がUでもBでも変わらず、分母の基数が小さくなっただけ純粋に(?)Pr(A|B)は上昇します。このとき集合Aは集合Bの部分集合である、という状態だと理解できます。
実際に確認しましょう。要素の白丸を移動して「AかつB」の基数を4+3=7、「AかつnotB」を3-3=0にすると(「B」も6+3=9なので)Pr(A|B)=7/9=約0.78です(ちなみに「尤度(likelihood)」はPr(B|A)=7/7=1、以前は4/7=約0.57と、いうことはコレってAがBの部分集合である率?)。確かにPr(A)=0.7に対して上昇はしました。以前の約0.67よりは大分マシです。しかし約1.11倍というシミッタレタ結果には満足できません。
ナンパ師が言っていた「(kitsonのバッグは)みんな持ってるじゃねぇか」問題が発生しています。
「AかつnotB」を空にしたので「notAかつnotB」だけが「notB」になったのですが、その基数がわずか1だったのでUからBに範囲を絞ってもあまり変化がない、と。「片っ端から行けってかオイ」というようにscreeningした意味が無くなってしまいました。
事前確率、事後確率の趣旨からいって「A」と「notA」の間で要素の移動をするわけにはいかないので、集合Bがらみを工夫するしかありません。たとえばkitosonではなくMULBERRYではどうでしょうか(錯乱)。(注:ランダムに選んだブランドですのでアレです、なんかごめんなさい:汗)それに応じて(?)集合Bによるuniverse=domainの切り分け方を変えて、これまでの変更点はそのままに、更に「notA かつ B」の要素を「notA かつ notB」に移します。
結果は...Pr(A|B)=7/7=1つまりエンカウント率100パーセント!!(大錯乱)。
えーと、集合Bのうち部分集合A以外の要素を外に出してしまったため、集合A=集合Bになってしまったのです。集合Bが全体集合の中から集合Aの要素を過不足なく完全に捕捉(?)できるとき、それは両集合が一致しているということになるんでしょう。ある集合が(全体集合に対して)AとBという二つの側面を持っていた、ということかと。
あー...

前回は「関数(写像)」の意味のブレについて言及しました。そしてλ記号を使った関数表記、モンタギュー文法による自然言語への応用等々について簡単に触れる中で「関数とはfなのかf(x)なのか問題」(?)も勃発。今回はそのあたりからアレコレしてみようと思います...。
とりあえず手近にある(あんまり専門的じゃない)ものに何て書いてあったかの確認です。
まず1冊目は計算機関連。
a value that depends on one or more arguments in such a way that, for any particular set of arguments, the funtion has only one value. For example, the positive real square root of a number is a function of that number. The sum of two numbers is a function of the two numbers. A function need not exist for all possible arguments; for example, negative numbers have no (real) square roots.(p.131)
引用は『Dictionary of Computer Terms』(Downing, D.et al,1995)にあるfunctionという項目のin mathematicsの部分から。傍線は引用者によります。
最初の傍線部では(いくつかのargumentに対して)functionがひとつだけのvalueを持つと書いてあります。たぶんright-uniqueという条件について述べているのでしょう。
で、最初の例示では「ある数に対する正の実数の平方根」がその「ある数」のfunctionだといってます。傍線をつけた次の例でいうと「the sum of two numbers」(=出力)が「the two numbers」(=入力)の「a function」だとか。
入力をx、出力をf(x)とすると「f(x)はx(←平方根のと違って和の例では変数が二つあることになりますけろ)の関数である」と言っていることになります。そういえば(読み飛ばしてましたけど:笑?)引用部分冒頭で「a value that depends on one or more arguments」って書いてますから「関数とはa valueである」という認識なんでしょう。「f(x)はxにともなって変化する値なので関数である」ってことかと。
むむむ...前回紹介した『関数のはなし 上』(大村平、1976)では旧来の「関数」にせよ現行の「関数(写像)」にせよ、いずれも「対応関係」のことでした。それと比べて「関数とは(関係ではなくて)value=値である」というのは随分話が違います。
なんだか重大な問題の気がしますが、ここでは深掘りしないでとりあえず留保しつつ別の事例もみてみましょう。
と、その前に一応確認しておきますと、三番目の傍線部でleft-toalという条件はどうでもいいんやで、と言ってます。「負の数」は「実数の平方根」を持ってないんやで、と。 説明をどちゃくそ省いてますけど、たぶん「平方根(=f(x))は実数(をdomainとする)xの関数(ていうか「xに対応した値」?)なんだけど、xが負の数のとき、それに対応する平方根は虚数になっちゃうんで、(codomainも実数に設定していたら)xに対応した平方根が存在しない場合があるんだけど、そこは気にしないでいいから」みたいな話なんじゃないかと。部分関数を許容する考え方ですね。
てか、んー、細かい(?)ことはさておき、やっぱ「関数」が「対応関係」じゃなくて「対応値」の意味になっちゃってるとこがなあ...。
そんで2冊目は義務教育範囲の数学分野。
When y is the function of x and expressed as y equals ax squared, y is said to be in proportion to x squared.(p.136)
引用は『英語対訳で読む「算数・数学」入門』(Patton,G.:2014)から。「y is the function of x」とありますのでyつまりf(x)がxの関数である、といっています。こういう言い方はどうやら「yはxの二乗に比例する値である」の「二乗に比例する値」を「関数」に置き換えたものっぽいです。1冊目と同じく「関数」を「対応関係」ではなく「対応値」とみてますね。
3冊目は高校数学教育関連。
たとえば、ある観測点についてみると、時刻xが変化するにつれて気温yも変化する。このように、ある数値xが変化するとそれにつれてもう1つの数値yが変化するとき、yはxの関数であるといい、変化する値xやyを変数という。気温yは時刻xの関数である。やかんの水の温度は加えた熱量の関数である。
xからyが決まることを、式ではy=f(x)などと書き、yは関数f(x)(エフエックス)であるという。
熱を加えると水の温度が上昇するというのは物理的な因果関係であるが、時々刻々の気温をきめる因果関係はややこしい。また時刻が原因で株価が結果であると考える人はいない。関数の概念は因果関係にかぎらずもっと適用範囲が広いのである。何らかの仕組みでxからyがきまりさえすればよい。(pp.39-40)
引用は『数学の小事典』(片山孝次他、2000)の「関数」の項目から一部抜粋です。傍線は引用者が付けました。
最初の傍線部にある例示からは上の二冊と同様に「f(x)はxの関数である」式の主張が読み取れます。またニ番目の傍線部で「因果関係」も含む関係において「関数の概念」が適用できるという話が出ています。
これは「関数(の概念)」と「(因果関係などの)関係」の間になんらかの係わりがあるという指摘だと読み取れますが、関数=関係ということは言っていません。何かと何かが連動して変化する「関係」そのものではなく、ある具体的な(?)数値となんらかの関係を持って連動する「対応値/出力値」のことを「関数」と呼んでいるようです。
読み進むと別の箇所で「関数とは数値である」旨を断言していました。例によって傍線は引用者によります。
もともと関数という言葉は、英語のfunction(ファンクション、機能)を中国で音訳した「函数(ハンシュウ)」という文字を使っていたが、「函(はこ)」からでてくる数、という意味では、まことにうまい訳であった。残念ながら「函」が当用漢字にないので「関」数になったのであるが、これは「関係」している数、と理解すればよい。(p.40)
傍線部をみると「函数」「関数」どちらであっても「数」を意味していると説明してます。まだ三冊しか確認していませんが気が滅入るというか混乱してきました。こんな解説ばっかりなんでしょうか?
4冊目は、2冊目と3冊目を併せた領域を扱う数学教育分野のもの。
ある規則(数式や表を含む)によって定められる対応関係のうち、「もとが決まれば対応の相手がひとつだけ決まる」ものを、関数といいます。対応とか写像とも呼ばれます。また、対応づける「働き」に注目して、「作用」と呼ばれることもあります。(p.67)
引用は『家庭の算数・数学百科』(数学教育協議会、2005)にある関数の項目から「[2]数学で:」の一部抜粋。right-uniqueな対応関係が関数であるとしています。left-totalは気にしてません。大村1976でいうところの「今様の関数」定義です。
というか、ここにきてようやく「関数」を「対応関係」だという説明が見られました。ほっとするとともに、それじゃあ前三冊(特に同じ分野の前ニ冊!)は何だったんだ?と不信の念も沸きます。
ところで同じ項目の「[1]自然科学で:」には以下のように書いてありました。
2つのもの(量、数)のうち、一方xが決まると他方yが決まるという関係にあるとき、「yはxの関数である」といいます。たとえば一定の温度のもとで、気体の体積Vは気圧pの関数です。(p.67)
「関数は対応する数値である」流の定義を「自然科学」での用法と考えているようです。つまりこんなふうに関数を理解するのは「数学」ではない、ということかと。
5冊目もおそらく4冊目と同じ範囲の数学教育関連。
集合Aの要素と集合Bの要素との対応で、Aのすべての要素xに対して、Bの要素yがそれぞれ1つ対応するような対応fのことを写像または関数という。このとき、Aを定義域、Bを値域という。Aからうつってきたもの全体f(A)をAの像という。(p.84)
引用は『身近な数学の記号たち』(岡部恒治他、2012)から。「関数」の項目はなかったので「写像」から一部抜粋。
所謂「関数(写像)」の解説であり、right-uniqueだけでなくleft-totalにも言及しています。引用部分の最後に「Aからうつってきたもの全体f(A)をAの像という」とありますが「うつってきたもの」とはどういう意味なのか「?」です。対応fによって集合AからBへ何かが「移動する=移る」ということでしょうか。それとも集合Aの姿(?)が集合Bに「反映される=写る」という意味なのか。比喩なのか方言なのか何なのか(脂汗)。
またf(A)とf(x)の間に違いがあるのかどうかも気になります。xはAのすべての要素ですから、domainである集合Aに対応fを適用した場合も、その全要素であるxに適用した場合も恐らく同じ結果になるでしょう(視点が内包的か外延的か、の違いはあるといえばあるでしょうけろ)。両者は同じと考えてよいのではないかと。
で、この本の解説が正しいならば、f(A)=f(x)は「像」と呼ばれるものであって「対応f=写像=関数」ではないのです。それなのに、これまで列挙してきた中に「像が関数である説」が大手を振って堂々と存在していたのが奇妙でなりません。
6冊目も同様の領域。傍線は引用者が付けました。
高等学校になると、抽象的に関数そのものを扱うようになります。そのための記号として登場するのがy=f(x)です。これを普通に「yイコールエフx」と読みます。関数のことを英語でfunctionというので、その頭文字をとってf(x)と書くのです。xにfを作用させてyに変える機能だと考えると分かりやすく、これを工学的にx→y(引用者注:→の上にf)と書いて、xを入力、yを出力としても分かりやすいと思います。(p.95)
引用は『数学記号を読む辞典』(瀬山士郎、2013)から「y=f(x)」の項目より一部抜粋。
傍線部で関数を「xにfを作用させてyに変える機能」と説明していますが、前回言及した「米と水に炊飯器を作用させて炊きたてのご飯に変える機能」が関数であるというアカン比喩と完全に一致(滝汗)。特に「yに変える」のところがヤバゲ。
しかも「機能」である関数を「f(x)と書くのです」と言いつつ「y=f(x)」のyが出力だとも言ってるので、関数は「炊飯器」かつ「炊きたてのご飯」というカオスなことに。
関数の抽象度をもう少し上げると、関数とは数の対応の機能である、という理解にたどり着きます。この場合はf(x)のxを省略して、f:X→Yと書くことも多く、関数という言葉の代わりに写像という用語を使います。写像になると、xが入力であるという感覚は少し薄くなり、代わりに、対応のさせ方という側面が強くなります。(p.96)
読み進むと上記のようにも書かれていました。「関数」と「写像」を「抽象度」の違いで分けています。ただ、両者の違いが具体的にどこにあるのかは判然としない説明です。
それにしても「関数とは数の対応の機能である」だとか「f(x)のxを省略して、f:X→Yと書く」という記述はかなり(悪い意味で)気になります...。「省略」って...。(補足:関数「f:X→Y」においてxがdomain Xの要素、y=f(x)がcodomain Yの要素であるとき、関数fをλx.f(x)と書けます。λ式内のxは「仮引数(formal parameter)」としてのxであって見た目は同じでも変数xとは無関係です。この関数を変数xに適用する際に紛らわしいのでzに変えてλz.f(z)にしてみます。こういう操作を「α変換(α-conversion)」というのだとか。このときf(x)は(λz.f(z))(x)と書けます。仮引数zに変数xを代入して処理を進めることは「β簡約(β-reduction)」と呼ぶようです。で、話は戻って、関数fをλx.f(x)のように表すことを「λ抽象」と言い、λ記号の別名は「関数抽象子(function abstractor)」なのだとか。つまり「抽象度」は上がっているのだと思われ...)
実際にチェックするまでは色々な定義はあっても「関数は関係である」という点は揺ぎ無いのかと思ってました。それでいて「関数」を「f」ではなく「f(x)」とするときがあるのはどうしてだろう?というのが疑問の発端だったわけです。
どうやら「関数」を「f(x)」とするのは「関数は値である、しかも(実数の)数値である」という説に基づいていたようです。じゃあ「関係」にあたるfのことは何と呼べばいいのだろう(困惑)。
従属変数f(x)は独立変数xの関数(=xに連動した値)である
色々な言い方をしてましたけど、まとめると(?)上記のようなことかと。要するに「関数」を「従属変数(dependent variable)」の意味で使っているんでしょう。
「独立変数」と「従属変数」の間にある(なんらかの規則に基づく)「関係」のことを「関数」と呼ぶのであれば、それぞれの変数を要素として持つ集合間の関係が「関数」の条件を満たす場合もあるでしょうから、それは「関数」(と呼んでも差し支えない場合が多い)です。しかし「従属変数」を「関数」と呼ぶのは許容できません。明らかにおかしい。
しかし、こうした間違いであるはずの内容で「関数」を説明している本が、希で極端なトンデモ本という感じでもなく存在している事実があります。書き手もデンパな人ではなく数学の専門教育を受け、大学などで数学を教えているような(知識や能力に折り紙つきの)マトモな方々です。
ワ・ケ・ワ・カ・ラ・ン
ていうか、「関数f(x)」という言い方は(俺ちゃんの記憶していた通り)数学教育において一般的なものらしいことが確認できます。
f(x) は,関数のニックネ−ムです。
f(x) の fは,関数の「名前(ニックネ−ム)」です。(関数 functionのf)
f(x) の(x) は,それが「xの関数」ということを示しています。
(略)
また,「関数f(x)」という表記は,問題文などでも使われることがあるので,意味をしっかり押さえておきましょう。
「f(x)」も「f」だけの場合も同様に「関数のニックネーム」だと言っています。「f」が「関数」を表していて、そのfに「(x)」の部分を付けることで「xの関数」であることを示すと。「f」だけだと「fは〜の関数」と「ナニナニの」部分が未定な(不完全で抽象的で一般的な?)関数を表現していて、「f(x)」と書いて初めて「f(x)はxの関数」というように「ナニナニの」が定まった具体的な関数を表すといいたいのでしょうか。もうちょっと詳しくいえば「f(x)は変数xを使った式で表される関数」とかとか?
ただ、こういう概念(?)の呼称としては、いずれにしても「関数」ではなくて「従属変数」の方がしっくりきます。繰り返しになりますけろ、なぜ「関数とは関係である」というもっとも基本的で本質的な定義をこれほどまで蔑ろにしまくるのか?がわかりません。
もうこうなったら禁断の下衆パー能力で推察するしかないようです。ゲスゲスゲスguess...(チーン!)。
f(x):=変数xで表現した「関係」式
このとき「関係」が「関数」ならば
「関係」式は「関数」式ともいえる
∴f(x)は「関数」(「式」は略した:テヘペロ)
こんな感じかと。初っ端から「f(x)は関係式で定義できるんだからこれはもう関係そのものだね!」という方向にもってく詭弁というか誤魔化しというか大混乱というか。上で書いたよりもうちょっと真面目にいうと「xとf(x)の間の関係が具体的にどういうものであるかはf(x)をxによる関係式で定義した部分に(のみ)集約される。だから関数をf(x)=関係式、あるいはf(x)によって表象することに何ら問題はない」ということかな。
で、ゴッソリ欠落しているのはdomainとcodomainへの、つまりxやf(x)が属する集合への考察です。「数」的なものだけを扱っているときには、そういう観点が全く欠落していても案外誤魔化しがきくのは確かな気もしますけろ。
「関係式」重視が「関数とは何か」の認識を歪める、ということを指摘する意見も実際にあるようです。
関数を単なる独立変数xと従属変数yの関係とみなす。個々の具体的事例において実験、観測を重ねることによって、xとyの規則性を見出し、その結果yをxの式で表して、関数を決定したする(引用者注:原文ママ)。あたかも実験、観測によりある関係式を類推し、それを式で表現すれば関数がわかったことになる、とする。このような指導は確かに重要で推奨されなければならない一面であるが、"教師の側の関数の理解"としては片手落ちの感は否めない。その側面だけでの強調は、教師の関数指導としては不十分であるのみならず、数学における関数のもつ意味の本質をとりそこなった、いびつな形の教育とならざるを得ないであろう。(p.65)
引用は『写像・選択公理論』(溝上武實、2006)から。傍線は引用者による。
変数間の対応における規則性を認識して式で表現する訓練をしても関数の理解は深まらないというようなことを言っています。むむむ...。
自然界に存在する現象などを数値化して、それと別の何かとの間にどんな関係があるかを明らかにしようとするとき、傍線部にあるような「ある関係式」が発見(?)できれば十分に目的は果たせます。そういう意味で独立変数のことは「説明変数(explanatory variable)」などとも言い、パーペキに従属変数を説明というか記述(?)できるものを使って関係式が書ければすっごく便利であることは間違いありません。
簡単な例でいうと、「円の面積」を従属変数yとして独立変数xである「半径」を使って表現した関係式なんかは小学生でも習ってた気が。関連するものでもっと簡単なのをいえば「直径」を従属変数yとして「半径」をその独立変数xとする、というのも関数といえます。
「三角形の面積」を従属変数にすると、独立変数は「高さ」と「底辺の長さ」です。複数の独立変数があってもこれを変数の集合と考えれば、というか日本語では変「数」といってますけど別に数じゃなくてもいいので「(高さ、底辺の長さ)」というペアの集合をdomainにして「面積」をcodomainにすればいつものパターン(?)に収まります。
直径と半径の関係はf(x)=2xつまり前回シツコク例に使ってきたやつそのままです。この関数をf(x)が独立変数になるように変形したあと両者を入れ替えてg(x)=x/2(逆関数の関数名はfの右上に-1って書くのが正書法?だと思うけろアレですんで...)とするとこれは「逆関数」になります。
一方f(x)=2xにおいて、たとえばf(x)=4というcodomain集合のひとつの要素に関して、これに対応するdomain集合の要素を見つけることを(たぶんですけど:笑?)「方程式を解く」っていうんじゃないかと。4=2xのxを特定することがそれっすよね、みたいな。ちなみに逆関数を使うといかなる「直径」の値についてもg(4)=4/2=2と自動的に「半径」を導き出せます。(補足?:一般的な1次関数f(x)=ax+bの逆関数はx=(f(x)-b)/aよりg(x)=(x-b)/a。一般的な1次方程式の解の公式はax+b=0を想定しているのでx=(0-b)/a=-b/aです。あと、どちらもaが0でない場合に限られます。為念)
統計学でも「回帰分析」で得られる「回帰式」が1次関数そのまんまだったり(故にアレを「方程式」と呼んじゃダメだと思うのですが、従属変数を関数と呼ぶのがスタンダード?だったり数学界はお題目と行動が不一致なんで、気にしても意味なさそう:笑?)(←「方程式」は英語だと単に「equation」つまり「等式」なので「=」が入ってる式はみんなequationだから回帰式だろうがなんだろうが「方程式」だという理屈か...クソが...ちな「方程」は『九章算術』の第8章の名前で連立方程式を扱ってるんですと...つかそんなら分類は「等式」と「恒等式」だけでよくね?なんで「方程式」とか呼ぶ?ああん?クソが...)(←しつこくてわるいんだけどさ「f(x)=(λz.2z)(x)=2x」みたいな式はどう分類するわけ?変数がどうでも常に成り立つよね?f(x)のところをyとかって書くと方程式だけどf(x)なら恒等式??そんな基準でいいの???)もするので、やっぱり従属変数と独立変数の対応規則を関係式に表現する部分が「関数」の本質と思われてしまうのでしょう。
ていうか、俺ちゃんも前回からずっと「関数f(x)=2x」みたいに書いてますしおすし(←!)。
でも関係式さえわかればその関数が表現できたということにはならないのは、たとえば上であげた直径と半径の例でもそうですけど、domainやcodomainを暗黙のうちに「実数」だとしてはおかしなことになる(直径がマイナスの長さになるとか云々)ことでも明らかです。この点を瑣末な問題と見なしてウヤムヤにしていいのかどうか。
>> 関数と方程式の違い(YouTube)
上に引用した動画では「100円のアイスクリームを買ったとき」という状況で「おつり」を従属変数、「支払ったお金」を独立変数としてy=x-100という関係式を使った例をあげています。消費税が無いということは昭和63年以前か!みたいな指摘はアレなのでアレするとして(←?)見過ごせないのはグラフです。
>> 上の動画のグラフ
「おつり」も「支払ったお金」もこれを表す変数は普通に考えれば自然数の集合に属するはずです。でもグラフは両変数ともに実数を想定してますので例示したものをちゃんと表現していないことになるんじゃないでしょうか(ツケとかカードとかリボ払いとか色々アレコレするともしかして負の数とか小数もありかもしれませんが無理数は出てこないと思うんですけろけろ:汗)。だからといって現役中学生が塾でこの解説を聞いて「直線にはなりませーん!その図は嘘れーすっ!!あばばばば」と抗議してもダマットレと怒られるだけでしょう(怒られる理由は図の是非とは別のところにある気もしますが:笑?)。
前節で述べたように、写像f:X→Yは一列に選択されたXのすべての要素に対して、fを働かせて得られたYの並びであった。決して、選ばれたXの要素xに対してf(x)の要素が与えられることではなかった。選ぶ前からの全体像であることは繰り返し強調した通りである。(p.80)
引用は溝上2006から。傍線は引用者によります。
めちゃくちゃ長くなってきたので端折りぎみでいきますが傍線部にあるように関数の「全体像」に意識を置く必要があるのではないかと。
そんで唐突かつ理解不十分のまま関数と集合をごっちゃにして考えてみます(←!)と、f(x)=x-100という関係式のグラフはh:X×Y→{true,false}で書けます(関数をhにしたのは単にここまでで使っていない文字だからで、それ以上の意味はありません:汗)。h(X×Y)とかh(x,f(x))またはh(x)(f(x))みたいな。関数f:X→Yでちゃんと対応関係にあるxとf(x)のペアの場合にはtrue、そうでないとfalseを返す関数です。
んーと、domainがX×Yつまり直積のとき、これは(x,f(x))のありえる全組み合わせを意味しているので、y軸がf(x)でx軸がxという座標平面の場合、XやYが実数だと全面隙間無く埋められることになります。このうち前述の条件でtrueになる部分にだけ黒く塗ると、つまり「h(X×Y) is true」の集合とそうでない部分にuniverse=domainを二分すると、一本の直線が現れる、というわけです。
XもYも自然数の場合は分割されるuniverse=domainが「面」的なものではなく、等間隔で規則的に並ぶ点のようなものになります。しかも全面ではなく右上(=第1象限)だけ。そうした点々のうち「h(X×Y) is true」のものだけを塗ると実数のときの直線と同じ軌道上(?)に並んだ点が黒くプロットされる...云々。
てか、もうちょっとリアルに100円アイスを買うネタで「支払ったお金」と「おつり」の2項関係を扱うとですね、f=(X,Y,G)は以下のようになるはずなんですよ。domainとかは有限集合かと。
X={100,500,1000,2000,5000,10000}
Y={0,400,900,1900,4900,9900}
G={(100,0),(500,400),(1000,900),(2000,1900),(5000,4900),(10000,9900)}
100円を超えた金額をわざわざ支払いに使うのは、100円より高額の硬貨や紙幣を使うからであって、ってことは、現在日本で使用可能なものだと五百円硬貨、千円・二千円・五千円・一万円札というわずか5種類しかありません(二千円札と消費税無しは時期的に両立しませんが海外勤務で一時帰国かつ免税店で買ったということで...あと額面が違う記念硬貨の問題もあるけど...十万円金貨とか...:参考→>>現在有効な銀行券・貨幣)。domainの要素は六つだけということに。(codomainを自然数に設定して、その部分集合であるf(x)またはf(X)、つまり像であるrangeと区別する手もある気がしますが、そこはアレで...)
この2項関係fは条件を満たしているので「関数(写像)」です。独立変数xと従属変数y=f(x)の適切なペア(x,f(x))の集合であるグラフGは、これまでの例と同じ図に6×6=36個の等間隔でなく並んだ点々のうち前例と同じ軌道上の6個の点で表せます。
domainが実数だったり自然数だったりすると(x,f(x))を全部書き出すことが不可能なので関係式による定義(?)だけしか使えません。こっちの例では極めて要素の少ない有限集合だったためどんな集合になるかの提示も可能でした。
ところで、扱う対象が「数」から離れるほど「関数」ではなく「写像」と呼びたくなる感覚があるらしいのですが、そうなってくるとルールが恣意的なため数式で表しにくくなって(たとえば前回例示した「食券システムの食堂」とか)、対応関係の記述は表やリストのようなものに頼ることになると思われます。そのようにして数の世界を対象とせず無限集合みたいなものを相手にしなくなる、っていうことは俺ちゃんタイプの文系ちゃんからすると具象化された(現実の?)対象を扱うようになる、と解釈するのですが、彼らは全然違うんですよね。それを「抽象度が上がる」って表現するわけです。
ふー...。まあ「数値化しろ!」っていうのは「フワフワしたこといってないで具体的なデータを出せ!」って意味でもあるから間違いではないのか。うーん...。
なんかすっごく疲れた。
悦楽と快楽は同じか異なるのか、その定義は曖昧なままおかれているようです。文学や哲学ではあえてそれを許容することで、言語のきらめきのようなものを獲得しようとします。ただし、曖昧な概念どうしが絡みあえば、解釈が幾筋にも分かれ、ある限度を超えると共通した意味をもたなくなり、言葉として使えなくなる危険性があります。数学ではそれとは反対の方向へと言語の構築を進めます。ひとつひとつの定義は、(そこまでに定義された語句を獲得できている人であれば)誰もが迷わず共通の概念にたどり着くように、ひととおりにしか解釈できないように書かれているのです。それが数学の語句の重要な特徴です。(p.23)
引用は『数学は言葉』(新井紀子、2009)から。傍線は引用者によります。
で、傍線部についてヒトコト。
とりあえず以上です(現在「下衆パー能力」がオンになっているので自衛のため発言を控えます:笑?)。

前回は述語論理のアレコレについて生成文法派の(ちょっと変じゃないかしらん?な)見解をサカナにつらつらと書きました。そんなこんなで、実は論理というのは集合としてだけでなく「関数(写像)」とも考えられることが確認できたっぽいです。
ただ色々ひっかかる部分は残ります。
例えば、むかし義務教育および義務教育っぽい(?)範囲の数学で習った「関数」と、これまで話題にしてきた「関数(写像)」はなんか違うっぽい気がしてならない、とかとか。
何事も結論から先に述べとくのが昨今の流儀ですんで(?)この疑問についても、まずは答えらしきものを以下に提示してから考察してみます。傍線は引用者が付けました。
古くから使われてきた数学上の概念を整理統合する立場からみると、連続的に変化するものどうしの対応を関数といい、一方を決めると他方がただ1つだけ決まるような対応を写像というような分け方は、あまり本質的な分類法ではなく、かえって、一方を決めると他方がただ1つだけ決まるか否かで分類するほうが、より本質的であり、どの分野にも共通な概念として妥当なものであることが、近年になってわかってきました。これは主として集合論の発展に負うところが多いのですが、ここでは余り深入りはしないことにしましょう。ともあれ、近代数学では、一方を決めると他方が1つだけ決まるか否かに重点を置いて数学上の概念を整理統合したために、「関数」をまったく「写像」と同じ意味に使うことになってしまいました。(pp.13-14)
引用は『関数のはなし 上』(大村平、1976)からです。かつては「関数」と「写像」は別の定義で使われていた、というようなことが紹介されています。
それぞれ「連続的に変化するものどうしの対応」と「一方を決めると他方がただ1つだけ決まるような対応」を指していたとか云々。この分類だと、扱う変数や要素のdomainとcodomain双方が「連続的」でなければ「関数」とは呼ばないことになります(離散的な記号システムである言語はこの意味では絶対に「関数」ではないことになります...よね?)。
それとは逆に「関数」には「一方を決めると他方がただ1つだけ決まる」という「写像」の性質は必須でないため、現在では「関数」にあたらないとされるものも含んでいた(例:「多値関数」のうち2値を扱うものとしての「2値関数」、たとえば与えられた値に対してその正と負の値を対応づけたもの、つまり絶対値関数の逆みたいなやつとかとか。ちなみに今は「2値関数」という語は「0または1」に対応づけられた関数のことを指すのが普通のようです...)らしいことが伺えます。
上記引用とは別の部分(p.11)で、語義の変化があったのは「20〜30年くらい前まで」とも書かれており、この本の出版年である1976年当時からみての話と考えれば概ね1946年から1956年くらいの間に(大村1976のevidenceが欠如した記述を信用するならば:汗)概念の整理統合が起こったようです。現在からですと59〜69年前の戦後期の話なんで、なんつかこんな感じにパイセン(注:先輩)が書き残してくれてないと事情わかんないよね、みたいな。
以下ちょい具体的な考察を試みます。
義務教育で習う最初の関数f(x)=axのような一次関数では変数xのdomainは実数であり、rangeであるf(x)の属するcodomainも実数であることから両方をR(←real number)として以下のように書けます。ていうか、domainなどについてそれが実数であることは暗黙の前提になっていて普段は明示されてなかったんですね。
f:R→R
このとき例えば具体的に定数a=2とします。矢印の左右をみますと、左から右への関係は「関数(写像)」の条件を満たしています。左のR集合の要素である変数xのすべてに対して、右Rの要素f(x)各ひとつに対応しています(たとえばx=1に対してf(1)=2とか、x=3.141592に対してf(3.141592)=6.283184などなどです...)から。
そして左Rと右Rの直積集合のうちf(x)=2xを満たすペアの集合、つまりグラフはy軸をf(x)、xをx軸とする座標中に傾きが2の直線として描けます(ところで、このグラフとあのグラフは同じ概念の別側面なのか無関係なのか...)。図を描くのは省略しときます(←!)。
f:N→N
またdomainとcodomainを自然数N(←natural number)に変えても「関数(写像)」であることに変わりはないようです。条件はクリアできています。ただ相違点として(実際には描かなかったけど:汗)上と同様に座標にプロットしたときに直線ではなく飛び飛びの点になること(具体的には{(1,2),(2,4),(3,6),(4,8)...}という点の集合。なお計算機言語では一般に自然数に0も含むため(0,0)も要素に加えます)があげられます。そしてf(x)=2xのf(x)が実際にとる値の範囲であるrange(←2の倍数、つまり偶数の集合{2,4,6,8,10,12...}。なお計算機言語では0を含む)と、設定されているcodomainの内容(←普通に自然数の集合{1,2,3,4,5,6...}。なお計算ry)も一致しません。
どうやらf(x)=2xという関数f(というか要素間の関係の規定?)は変わらず一貫していても、domainとcodomainをどうするかで色々と関係に違いが生じるのがわかります。たとえば有理数Q(←quotient)に設定すると、無理数にあたるところだけが途切れた感じにプロットされそう、とかとか(有理数は「可算無限」なので自然数と同じ「濃度」であると「カントールの対関数」で証明できて云々...)。
f:N→R
f:R→N
更に設定を変えてみて、例えばdomainを自然数Nにしてcodomainを実数Rにした場合でも、f(x)=2xという関係について、domainの要素に対応したcodomainは必ず1つ決まるので、これも「関数(写像)」として問題ありません。codomainが自然数だった場合と同じ結果です。
しかしこれと逆にRとNを入れ替えた関係では、domainに対応すべき要素がcodomain側には存在しないケースが多数生じます。実は大村1976の定義ではright-uniqueだけに言及していて、関数に必須のはずのもう一つの性質については触れていませんでしたが、その「domainのすべての要素にcodomainの要素を対応づける(=left-total)」という条件が満たされません。
こういうもの(=right-uniqueだけの関係)は「部分関数(partial function)」と呼んで広義(?)の「関数」に含め、ちゃんとしたものを「全域関数(total function)」(=left-totalかつright-uniqueな関係)と呼び分ける考え方もあるようです。たぶん、そういう諸々(?)を考慮して大村1976はright-uniqueだけを「関数(写像)」の性質としたのでしょう。
なにはともあれ、どうやら思っていた以上に数学界(?)では術語の(意味や用法の歴史に関する)整理がいいかげんな気が(呆)。たぶん人間の営み的なアレコレなんかと無関係で、絶対的かつ客観的な揺ぎ無い真理みたいなものを自分たちは扱っているのだから、そのあたりはいい加減でも別にどーでもいーめんどくせー的なオゴリがあるのではないかと(個人の感想です)。
とはいうものの、義憤は覚えつつも個人で整理整頓するにはあまりに面倒っぽいので出来るだけ目を瞑って先に進みます(←!)。
で、えー、そんな舌の根の乾かぬうちに唐突かつ蛇足ですが、大村1976では(俺ちゃんが考える言語と記号システムの問題にとって:笑?)「おっ!」なことが上で引用した部分の続きに書いてあったので御紹介しておきます。案外大事な問題かな?とも思うですよ。
ところで、この本で取り扱う関数は、1次関数、2次関数、三角関数、対数関数などが主で、いずれも「xを連続的に変化させると、それにつれて一定の規則のもとにyも連続的に変化する」ような昔風の関数が大部分です。なぜ、年月日と曜日や学籍番号と学生の氏名のように「一方を決めると他方が必ず1つだけ決まる」ような今様の関数を仲間に入れないかというと、それは次の理由によります。
年月日は1日単位のとびとびの数字です。そして、曜日は、日月火水木金土と7個の星の名前が並ぶのですが、この並び方に自然科学的な意味があるわけではありません。したがって、その並び方を丸暗記しておかないと、年月日との対応ルールが見当もつかないのです。(中略)したがって、こういう関数関係のルールは全くケース・バイ・ケースであって共通の特性がなく、一般論として採り上げるには不適な場合が多いからです。(pp.16-17)
傍線は引用者がつけました。大村1976で扱う「関数」は昔風の定義による関数で、つまり実数とか複素数のように連続的なものをdomainとcodomainにした関係に限ると宣言しつつ、その理由について述べています。
それは傍線部にあるように、「今様の関数」つまり「写像」では、扱う対象が「とびとび」で「並び方」に「自然科学的な意味」もなく、「対応ルール」も「丸暗記」を必要とする「ケース・バイ・ケース」なものであるためだとか。
すぐに気付くことと思いますが、この「今様の関数」の特徴こそ、もしかしたら「言語」を記述できるかもしれないと期待された側面です。つまり形式言語の研究で参照されるような「論理」「集合」「関数」システムは、大村1976の視点(=昔風の数学?)からは「一般論として採り上げるには不適格」とみなされてしまうことがわかります。
このことからは、「丸暗記」を必要とする恣意的な「ルール」の獲得に関する理論構築が、言語研究において重要な鍵となることが逆説的に照らし出されます(←ちょっと話が飛躍してね?←うるへー!字数の関係や!!)。生成文法派はここを「生物学的必然性」「生得的能力」による(故に恣意的でなく「自然科学的な意味」がある)から全然オッケーみたいに短絡しちゃってるんじゃないかと(個人の感想です)。
自然言語処理分野の人たちは生成文法派とは違った真っ当な取り組みをしているように見えまするが、その具体的なアレコレについてはまたいずれ機会があれば改めて...(←!)。
上述した内容では、関数(または関係)をf:R→Rみたいに書いてきました。しかしこれだけでは実際にはどんな関係なのかよくわかりません。もっと具体的(?)には、要素でいえばx→f(x)という内容があり、それはf(x)=2xからx→2xだったりするわけです。
そこで、こうした情報をもうちょっと効率よく(?)記述する目的で「λ記号」が導入されます。
しかしそれは、関数が入力-出力の関係(i.e.入力を何にするかによって出力が一意的に決まるという関係)であることに注目すれば、容易に可能となる。すなわちそれは、関数の入力部分と出力部分を並記することによって関数の関数性(i.e.関数自体)を示す、という方法である。(中略)そこでさらに、入力部分xを記号λと.ではさむことにより、fをλx.f(x)と表す記号方が採用されることになる。今後頻出するλ記号とは、このように関数の入力部分を明示するために導入された記号である。(p.13)
引用は『圏論による論理学:高階論理とトポス』(清水義夫,2007)から。傍線は引用者が付けました。
最初の傍線部で関数とは「入力-出力の関係」であるといっています。微妙に今まで見てきた言い方と違うのですが、これもたぶん広く使われている関数概念の説明のひとつです。で、すごく誤解されやすいっぽい。
>> 「関数という論理操作」?
このことは、著者の「関数」のイメージが、関数プログラミングでの「関数」と食い違っていることを示しています。関数プログラミングでいう「関数」は数学的意味での関数、つまり、「写像 f:A→B」であって、あくまでも始域 A の元と終域 B の元との 対応関係 のことであり、そこには(始域の元が終域の元に「なる」というような)「変化」などというものはありません。
なにやら関数の説明をする際に、入力を「米と水」、出力を「炊飯器(米と水)=炊きたてのご飯」、関数を「炊飯器」に例えるということをしている本があるらしく、上記引用先のサイトではそれを批判(?)する記事を書かれているようです。
なんつか、食べ物ネタで俺ちゃんが例えるなら「食券を差し出して料理を受け取るシステムの食堂」みたいなことを考えると思います。つまり、入力というのは番号が書かれた食券の集合{1,2,3,4}で、出力はそれに対応したメニューの品々の集合{f(1)=カレー、f(2)=ラーメン、f(3)=けつねうろん、f(4)=高級茶葉のみ選定したウーロン茶}とかとか。
で、たとえば「1」と書かれた食券を店のおばちゃんに渡して(=入力)、その結果「カレー」を受け取った(=出力)とき、まさかおばちゃんが食券を材料にしてカレーを作ったとは思わないですよね? そこには「変化」ではなく「対応」関係があるだけです。
ついでにいうと、この対応関係はあくまでこの店のシステムでそうなだけで、別の食券システムの店で食券番号「1」に対応したメニューf(1)が「カレー」であるかどうかは全くわかりません。ケース・バイ・ケースです。偶然一致することもあるかもしれませんけろ。
たぶん昔風(?)数学での一次関数f(x)=2xみたいな事例で、入力xと出力f(x)=2xの関係が「xから2xを算出できる」=「xが2xに変化する」みたいなイメージになっちゃってるところがアレなのかなあ?みたいな。ともあれ下手にクビを突っ込むとおっかないことになりそうな案件ですんで、これはこのくらいにして話をλ記号に戻しまする...。
(λ☆.2☆)△
(λ☆.2☆)(x)
=f(x)
=2x
上で引用した清水2007の二つ目の傍線部にλ記号は「関数の入力部分を明示する」ためのものだとありました。そこで関数をλx.f(x)という書き方で表すわけですが、これもちょっと誤解してしまいそうな杞憂を覚えます。
そんなわけで上にその点が明らかになるようなものを書いてみました。一次関数f(x)=2xを想定しています。
最上段のやつはλx.f(x)をf(x)=2xからλx.2xとしたののxを☆に変えて書いています。そして関数部分λ☆.2☆の右側に△があります。二段目では△の位置がxに変わりました。この位置に置かれたモノ(?)が関数に「適用」されるということを明示しています。ここでは変数xが適用されました。範囲を明確化するためにxはカッコで括っています。
で、この全体は三段目のf(x)とイコールです。つまりλ記号を使った表記は関数fの「f」そのものに該当し、その内容を直接的に示していることがわかります。(備考:俺ちゃんは義務教育っぽい範囲の数学では「f(x)が関数である」みたいにx込みで言われてた気がするので「f(x)は関数fに変数xが適用されたものであって関数fの出力にすぎない、場合によってはそれも関数かもしらんけどな」というのは「ファッ?!」でした。てか「fが関数」説の方があらゆる意味で理にかなってる、というかそう考えないとそこら中で矛盾しまくると思うねんけど、なんであんなこというてたん?次回書くと思うけろ数学教育界?っぽいとこの人らはいまだに「f(x)が関数」説やねんな。てか、掛け算の順序がどうこういうのんと同種の問題やろか...闇が深いわ:油汗)
そして(ちょっと話は前後するのですが)△位置のものをλ☆.で明示された☆=入力とみなして、それを出力部分にある☆の位置に代入する...という一連の流れによって(この場合では結局2xになり)四段目にも繋がるわけです。
こういうナニヤラによって、単に変数を関数に適用するのを表記できるだけでなく、関数を関数に適用するのやら色々と重層的で複雑な関係を表現することが可能になります。この先を延々解説していく余裕はないので一気に端折りますが、例えば以下のようなことが言えるようです。
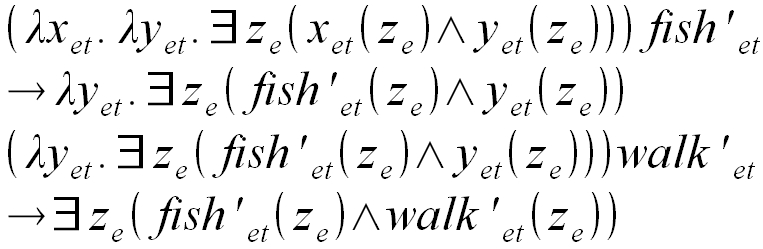
論理式は清水2007のp.37から若干改変して拝借(←!)。上ニ段が自然言語での「a fish」で、下二段が「a fish walks」を表しているのだとか(汗)。
えーと、まず最上段の式は「カッコで括られたλ記号部分を含む複雑な関数」および「fish'」に構造を二分できます。つまり左の関数に右のfish'が適用されることを示しており、またfish'は変数ではなく(内容はλ記号で明示されていませんが)それ自身が関数です。
fish'がλx.のxを入力対象(?)とし、量化子のついた出力部分のxに代入されて二段目の式になります。一段目左のややこしい関数が「a」という不定冠詞というか決定詞(determiner)を表していて、これが引数的なものとして名詞「fish」を(他動詞が目的語を「とる」みたいに)とる、という感じ。(補足:決定詞が単なる名詞句の指定部ではなく、こちらの方がXバー理論における主要部である、という説とも合致してますね...参照→DP analysis)
三段目はこの結果の(つまりa fishをλ記号で表記した)関数にwalk'という動詞を表す関数を適用しています。上と同じような手順でλy.のyにwalk'を代入した結果、四段目のようになりました。
集合論的に言えば、「fish'という性質である」かつ「walk'という性質である」ようなzが存在する、ということを表しています。a fish walks...ってそういうことだったのか(驚愕)。魚であり、なおかつ歩く、ようなモノが存在する...みたいな。
さて、故意に無視してましたがeとかetとかいう添え字みたいなのがついてます。これはタイプを表していて基本的にはeとtだけしかありません。eとtを組み合わせたetはe→tの略です。入力のタイプがeで出力のタイプがtであるような関数、を意味します。
ですのでetタイプのfish'やwalk'は、fish'(z)などとしてe(←entity)タイプであるzを適用されるとtrueかfalseを出力する...(備考:たぶん集合論でP(x)が実際には「P(x) is true」という真の場合だけを示していたようにfish'(z)も「fish'(z) is true」であるようなzを出力する、ってことで添え字がtだと思われ...)という関数なんじゃないかと。そして、λx.のxなどについているetは、etタイプのものしか入力と認めないという意味だと考えられます。
こういう文法というか言語モデルを「モンタギュー文法」というようです。清水2007の例はその超簡易版だとか。それでも笑うしかないくらい複雑に見えますが、fish'とwalk'適用後の四段目をみると、結局「a」は単に「存在記号+変数z」に落ち着いてしまってますし、案外アレかもしれません。(補足:たぶん一段目左の決定詞を表すλ式は「変数zが適用されることは既定だが内容は未定の関数」同士を「かつ」で結ぶ構造が組み込んであって、つまり関数タイプを二回適用するように準備されていて、その上で決定詞の「a」が不定冠詞であることから存在記号の量化子で括ってあるんじゃないかと)
問題は複雑さよりもむしろ「えー、そうかなー、あたしそんなこといったかなー」(cv:金田朋子)みたいなことなんじゃないかと。モンタギュー文法で表現されたことと、自然言語の文が意味していることの間には「すっごく」齟齬があるように思えてなりません(個人の感想です:本件三度目)。
あー。
また間違った!!!!すみますみません。
上で「f(x)は関数fに変数xが適用されたもの」って書きましたけど、「f(x)は関数fを変数xに適用したもの」って言わないとダメっぽいです。つまり「適用する」は「変数xに対して関数fを」前から後ろに(?)作用させる意味で使わないとダメなんだとか。色々確認してみてもみんなそういう使い方でした。ぬう、そうだったのか。
しかしですよ...たとえば上で引用したリンク先のドッキングは「1号機が2号機にドッキングする」のか「1号機に2号機をドッキングさせている」のか...なんか噴出しているのは2号機ですしおすし。
ともあれ(?)何の「実体」もないところに(概念である)「関係」だけが先行して存在しており、遅れてきて現れた「実体」が「関係」に突っ込まれて云々、みたいな考え方は常識(?)的には確かにちょっと変かもしれません。それを変と思わない環境で育ったのでアレやった(滝汗)。
そのあたりも含めて次回もこのネタひっぱるしかなさげだぬん。

前回まで述語論理に関する最低限の道具立て的なものについて扱ってきました。言及した内容だけではまだまだ全然足りてないですけど(滝汗)。それでこの先「n項関係」や「写像」云々について触れていかねばならないのですが、とっかかりとして「生成文法派が語る述語論理」について簡単に触れてみます。
先回りして大まかにいうと、前回確認したようなレベル(?)の古典的(=アリストテレス風?)述語論理は自然言語の文法記述(?)に使えるが、それ以上複雑な(?)述語論理はアカンということらしいです。なんか「?」ばっかしですが(笑?)。
We see that there is an asymmetry between the subject and the object. The subject and the verb are in separate phrases, but the verb and the object from a single phrase, which we call a verb phrase. In general, then, subject-verb-object sentences have the form (13), where we now indicate the category of a phrase by a subscript on the bracket, NP for noun phrase, VP for verb phrase, and C for clause:
(13)
[_C NP [_VP V NP]]
(p.54)
引用は『Language and Problems of Knowledge: The Managua Lectures』(Chomsky,1988)から。傍線は引用者が付けました。
さて、どういう議論なのかこの部分だけからはわかりにくいでしょう(汗)。とりあえず傍線部にあるように、subject-verb-objectという三つの部品から出来ている文はsubjectとVP(=verb-object)に分割される、という主張と理解できます。引用冒頭文にあるsubjectとobjectのasymmetryというのもこのことです。つまり、subjectに比してobjectはverbと強く結びつくのだ、と言いたいみたい。
述語論理ではたとえばP(x)のように命題文を表現しました。このときxがsubjectでPはpredicateです。predicateについて品詞(?)的な縛りはありませんので「is mortal」などのような形容詞だけでなく動詞も使えます。
動詞が他動詞であってobjectが必要になる...つまりsubject-verb-object構造の文を、たとえばVerb(subject,object)みたいに記述(更に略してV(s,o)とか、カッコ内を引数としてV(a_1,a_2,...)とかとかに一般化することで他の文型(?)にも対応)しても良いのではないかという発想が当然出てきます。でもそれは間違いだと言いたいらしい。
There is a good deal of independent evidence converging on this conclusion, one piece of which I have just presented. It is, once again, by no means a necessary conclusion. One might assume that a transitive verb simply relates two terms, its subject and its object, with no asymmetry of structure. In fact, that is the assumption made in the construction of formal languages for the purposes of logic and mathematics, and it has often been proposed for human languages as well. Formal languages are constructed in this way for reasons of simplicity and ease in computational operations such as inference. But the evidence indicates that human languages do not adopt the principles familiar in modern logic. Rather, they adhere to the classical Aristotelian conception that a sentence has a subject and a predicate, where the predicate may be complex: It may consist of a verb and its object, as in (12) and (13), or a verb and a clausal complement, as in (8b).(p.54)
先の引用にすぐ続く部分です。傍線は引用者が付けました。
二つ目の傍線部にあるように他動詞が二つの項(=subjectとobject)と単純に(なんら両者に差が無く)関係している、という仮説もあり得ることを認めています。そして、この仮説は形式言語の前提であるだけでなく人間言語にも適用されてきたとも述べます。
しかし三つ目の傍線部で、この仮説が人間言語(=「自然言語」? )では使われていないとindicatesするthe evidenceがあるようなことを言っています。このthe evidenceって何じゃろ?
最初の傍線部にそうしたもののひとつをI have just presentedだと書いています。上で引用した箇所の前にそれらしきものが書かれていましたので(述語論理の話とは逸れてしまいますけろ...)以下に掻い摘んで紹介してみたいと思います。
ええと、まず「束縛理論(Binding Theory)」というものがあります。生成文法派が主張する普遍文法を構成する下位理論のひとつです(補足:少なくともGB理論時代には)。これは「照応形(anaphor)」「代名詞類(pronominal)」「指示表現(R-expression)」に関して先行詞がどうあるべきかを規定します。参照→『チョムスキー理論辞典』(1992)pp.55-59
二つ目の引用部分最後にある(12)という例文について、この理論に則った場合にsubject-verb-objectからなる文は「(subject)(verb-object)」と「領域(domain)」が区切られるべきであって「(subject) verb object」というように(asymmetryではなく?)考えることはできないと言っています。この例文(12)はスペイン語ですが(補足:ニカラグアでの講義録なので例文はスペイン語)英訳も併記されていますので以下にそちらを引用します。
[The man [who wrote the book]] [destroyed it].
このとき代名詞itの先行詞がthe bookであるためにはpronominalに関する束縛理論に合致しなくてはなりません。Chomsky(1988)p.52に書かれたそれは、領域内で代名詞は束縛されていてはならない、というような内容です。
(10)
A pronoun must be free in its domain.
例文(12)では「The man who wrote the book」というsubjectと「destroyed it」というVPとで(階層構造の最初の分岐が)二つに分けられているため、後者のdomain内でitは他の語や句にbindされておらずfreeであるとみなされます。よって別domainの下位区分にあるthe bookを先行詞とすることができる...ってことかと。
「who wrote the book」はそれでひとつのdomainだそうですから規則の文言だけを字義通り(?)に受け取ると、別にVP作んなくてもitはfreeじゃね?と思ったりもするのですが、そうではないようです。階層構造にしたときに下位に含まれているのは全部同一domainという考えなんでしょう。
色々書いてみましたが、要するに「The man who wrote the book destroyed it」という例文は「[The man [who wrote the book]] destroyed it」(=階層構造の最初の分岐が三分割になる解釈)ではなく(12)のように解釈(?)されねばならない(なぜならそうでないと生成文法派の提唱する束縛理論にとって都合が悪いから:笑?)と言っていて、それが(生成文法派の主張する「verbに対してsubjectとobjectがasymmetryだ」という意見のひとつの)evidenceだそうなのだとか。
なんつか、うーん...。asymmetry云々の妥当性はとりあえず置いておいても「それってカリー化(currification)じゃだめなんすか?」とは聞いてみたい。
f(x,y)=f(x)(y)
関数型古典高階(述語?)論理のようにλ記号を使う論理だと上の式が成り立つため、複数の変数(引数?)をとる関数を、複数の一変数関数と見なせるのだとか。参照→『圏論による論理学:高階論理とトポス』(清水義夫,2007)pp.39-40
・・・と、ハナシが先走ってしまうので、このあたりについてはとりま忘れてください(←!)。ただ論理に関する意見が変っぽいことだけは指摘しておきたいかな、っと。マルコフ連鎖に関してもそうですが、あの人たちの他分野の知見に対する敬意の無さ、理解の変テコリン具合みたいなのがすごく気になってしかたがありません(個人の感想です)。
あと蛇足ですがChomsky(1988)ネタの最後に、この件についての更なる生成文法派的超理論展開を御堪能いただきたく存じます(笑?)。傍線は引用者によります。
The asymmetry, a property of human language but not a neccessary property, is once again surprising. It gives rise to Plato's problem once again. How do children acquiring a language come to know this fact? It might be thought that they discover the fact as we just did, but that is certainly false. Our path of inquiry involved conscious inference based on the explicitly formulated principle (10), and we made use of evidence that is surely not generally available to the language learner. In fact, the line of argument just presented, which leads to general conclusions about the language faculty, would not be convincing unless it were supported by similar evidence from other languages as well, and the child does not have evidence from other language available. (...) Rather, as language grows in the mind/brain, the child comes to incorporate the principle that a transitive verb and its object from a phrase, as a matter of biological necessity; and then principle (10) of binding theory, which is part of the language faculty as a matter of biological necessity, determiners the interpretation of such sentences as (12) by a computational process of unconscious inference.(pp.54-55)
最初の傍線部でsubjectとobjectがverbに対してasymmetryであることが人間言語の性質なんだけどnecessary propertyではない、としています。このときのnecessaryは「論理的に必然(的な帰結であるような)」というニュアンスかと。英語力アレなのでアレですけろ。
そうでなければならない理屈はないのにそうなってるから不思議だなあ...みたいに三味線弾いてます。そして二つ目の傍線部にあるように、子どもちゃんたちはどうやってthis factを知るんだろう?どうしてだろう?とか言ってます。いつの間にfactになったんや...(白目)。
三番目の傍線部ではaymmetryのevidenceとして「他言語でもそうだから」というのがあったことがわかります。そういえばスペイン語と英語で同じようなことが言える、ということは示していたのでした。だから人間言語にとって普遍的であると。
確かにそういうevidenceは子どもちゃんには確認できません。また引用中省略した部分に書いてあったことですが、上で見てきたような束縛理論に基づいてアレコレ考えることも我々(←?)と違ってできません。
そして最後の傍線部で明らかにされる「evidenceに基づいて判断できないのになぜ?」という疑問への答えは(俺ちゃんからすると超論理すぎて:笑?)驚くべきものでした。
subjectとobjectがasymmetryだとわかるのはas a matter of biological necessityだと。論理的な必然ではないが実は生物学的(?)必然性なのだと。そして束縛理論もそのようなthe language faculty as a matter of biological necessityであり、故に子どもちゃんたちはそれを無意識のうちに使用して我々(←?)と同じくthe factを知るのだとしています。
いつもの、といえばいつものですけどね(←驚いてないやんけ!←毎度のことでもビックリはしとるで...)。万能句「根岸の里の侘び住まい」みたいに「生物学的必然性」「生得的能力」を使ってケリをつけるといいますか。
上で長々書いて(エネルギーを浪費して:笑?)しまったのでここは手短に済ませます。
それでは語順以外に何が目立ったかと言うと、動詞と目的語の結びつきの強さです。これは、ここにはHinds(1973)を代表的な例として挙げましたが、(生成文法の歴史に詳しい方はご承知のように)この時代は、いわゆる生成意味論(Generative Semantics)というものが勃興していた時代と重なっており、生成意味論というのは、自然言語の基本的な構造は述語論理学で用いられているものと同一であると考えたわけです。述語論理学では関係というものは、まずXとYがある。そして、それに関係Rというものが定義されるわけです。ここで重要なことは、XとYの間にRに関しての違いが何もないことです。それに対して、もっと古典的なアリストテレス流の考え方では、述語があったら、それに対して何かが、例えばYがくっついていると考えます。そしてその外側に、例えばXというようなものがあって、全体としてひとつの命題を成している。自然言語の分析のモデルとしてアリストテレス流の考え方と述語論理学の考え方とどちらを採用するかは、純粋に経験的な問題です。生成意味論は述語論理学の考え方を採ったわけです。ところが、ここでは省略しますがいくつかの証拠が挙がって、どうも自然言語の文というものは古典的なアリストテレス流の構造をしているのではないかと言われてきました。このことは、もし正しければ、経験的な発見です。(pp.49-50)
引用は『自然科学としての言語学:生成文法とは何か』(福井直樹,2001)からで傍線は引用者が付けました。
最初の傍線にある「語順以外に」というのは日本語の特徴について言っています。日本語と英語で語順が違うというのは誰でも知っている話かと。引用部分の内容からは著者の主張がちょっと読み取りにくいかもしれませんが、日本語では英語よりも動詞と目的語の結びつきが弱いと言いたいようです。
つまり日本語には英語における「VP」のようなものは無いのかも?と(生成意味論とかの初期の生成文法理論時代には)思われていた云々という話がしたいみたい。この引用部分のあと「VP移動」について説明していますしおすし。
ただ、その話をする前提として述語論理等々について語りだしたものの、途中でかなり面倒くさくなって端折ってしまったのかも(←下衆パー能力で推察しました)。
そんなこんなで(?)二つめの傍線部で「関係」について述べていますが説明がコンパクト(笑?)すぎてワケワカラン感じになっちゃって...。しかたがないので僭越ながら俺ちゃんが色々補足してみます(ただしこれまで以上に「独自研究」色が強い=知識や理解がウロですんで、そこんとこヨロシク!!)。
まずは述語論理でP(x)などと書けるときのPが一体何を表していると考えられるのか?という点についてちょっと振り返ってみましょう。
ひとつはこれまで述べてきたように「(xの)性質(property)」です。ある性質を持つxをtrueとし、そうでないものをfalseとすることで集合を作りました。別の視点では「条件(condition)」ともいえます。
このP(x)的なものの引数を増やして、例えばR(x,y)としたとき、Rは「(xからyへの)2項関係(2-place relations)」だとされます。引き続き性質や条件と呼んでも間違いではないと思いますが(ちょっと工夫がいるでしょうけろ:汗)。
変数xが属する「定義域(domain)」をX、変数yが属する「変域(codomain)」をYとします。変数x自身も「定義域(domain)」ですが変数yについては「値域(range)」と呼んで区別するようです。当然ですがここでいうdomainはChomsky(1988)に関してあれこれ述べた中に出てきたdomainと全く関係ありません。「論理の箱庭」で出てきた変数xのuniverseにあたるものです。
このときRはXとYの「直積(Cartesian product)」のうちRという関係の性質/条件に合致するものの集合である「グラフ(graph)」Gと同一視して良いようです。要素集合からの外延的な定義みたいなもんでしょうか(←質問か!)。ですからRは(X,Y,G)で表せるのだとか(←伝聞か!:呆)。
抽象的な話をしててもアレなので適当な例を。ちなみにR(x,y)はxRyとも表記します。
X={1,2,3}
Y={1,3,4}
X×Y={(1,1),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,3),(3,4)}
G={(2,1),(3,1)}
x={2,3}
y={1}
この例でのxRyはx>yを想定しています。つまりRは「xはyに対して大なりという関係」だということです(別の解釈も可能かもしれませんが...)。
ちなみに「関係」は「写像(mapping)」や「関数(function)」であるとは限りません。「関係」がleft-totalとright-uniqueという条件を満たすときに限られます。つまりdomain集合からcodomain集合への(=左から右への)対応がdomainの要素すべて(=left-total)からそれぞれcodomainの要素のどれかひとつに対して(=right-unique)行われるという特殊な「関係」を「関数」(あるいは「写像」)と呼ぶそうです。
R: X→Y
Rを関数として上のように考えると、例としてあげたxからyへの関係R(=x大なりy)はleft-totalを満たしていない(=Xのうち{1}を除いた{2,3}しかYと対応していない)ので関数ではないっぽいです...などと言い切らずに言葉を濁してしまうのは、命題としてこういうものを扱うと、なんかちょっと事情が変わってくるような気がするからです(純粋に気分の問題です←!)。
というのも、たとえば以下のように考えたらどうなんでしょう。
R: X×Y→{true,false}
その場合にRを表す(Domain,Codomain,Graph)の値はこんな風になりそうです。
Domain={(1,1),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,3),(3,4)}
Codomain={true,false}
Graph={((1,1),false),((1,3),false),((1,4),false),((2,1),true),((2,3),false),((2,4),false),((3,1),true),((3,3),false),((3,4),false)}
DomainとCodomainの直積集合の要素のうち((1,1),true)とか((2,1),false)みたいなのはGraphでは排除されています。つまりright-uniqueという条件に合致しない部分が取り除かれているわけです。left-totalは満たしてます。故に関数だということです。
こうやって考えると大抵の「関係」は「関数」として扱えるような気がしてくるのですが、そのあたりどうなんでしょうか。なんか根本的なところで俺ちゃんの理解に変テコリンなところがあるせいのような気がしてならないので不安でありまする(←告白か!)。
あーっと、福井(2001)をすっかりほったらかしにしてましたが、まあ、アレです。二番目の傍線部で語られている「古典的なアリストテレス流の考え方」は、まさしくカリー化で言及した式の右辺的なもので、f(y)という一引数関数が引数に何か値が入った(?)状態で、これを仮にf'とするとf'(x)という一引数関数として機能する的なことを言っているようです。
前述したようにf(x,y)=f(x)(y)ですので、λ記号を使う論理の場合、福井(2001)で述べているような「述語論理学」と「古典的なアリストテレス流の考え方」の間に違いはありません。一般的にもそう考えるのが普通なんじゃないかと。(自分のことは棚に上げつつ:汗)何か再現の難しい変テコリンな理解の仕方をなさっているのではないかと下衆パーしてしまう衝動を抑え切れません(滝汗)。
あと生成文法派に特有の謎の用語といえば、残りの傍線部で示した「経験的」です。「純粋に経験的な問題」とか「経験的な発見」というのは一般的な「経験的」の用法とは大分ずれているようにみえます。これは「生成文法理論は経験科学だ」といわれるときに感じる「経験」への違和と同種のものですが、どうやら彼らは「脳内での思いつきにすぎない仮説を強弁してみて世間(?)の反応を見つつ(捨てる/もうちょっと強弁を続ける/新たに思いつく)等々の行為を選択する過程」を「経験」と呼んでいるようなのです。
そう考えると生成文法派の足跡が失敗仮説の死屍累々であることも(彼らの用法でいうところの)「経験」「科学(cargo cult science)」であるという主張に確かに合致しています。
次は「λ記号をつかう論理」か「ならば」を使った推論の話あたりをやりたひ。

前回の内容は「論理の基礎の初歩の途中」くらいで終わっていました。論理結合子のうち量化子には触れていませんし、P(x)やQ(x)やR(x)における変項xって何...みたいな問題にも結論は出ていません。
そういうわけで、まずはそのあたりの積み残しを処理していこうと思います。
さて、まずは前回使った「論理の箱庭」を再利用しましょう。

なんだかんだで上の楕円をP(x)、下のをQ(x)、両方の重なった部分をR(x)としました。P(x)が「八角形」という性質を持った要素の集合、Q(x)は「色付き」、そしてR(x)は「八角形で色付き」の集合でした。しかし、この説明(?)では言葉が少し足りていなかった気がします。
「八角形という性質を持った要素の集合」とは正確には「P(x) is true」である集合、というべきでしょう。他のものも同様です。「Q(x) is true」「R(x) is true」であり、こうしたもの同士を論理結合子で結んだ論理式で表せるものも「論理式ナニソレ is true」という条件に合致したものの集合ということになります(例えば「R(x) is true」は「[[P(x) is true] and [Q(x) is true]] is true」な集合のことです...よね?)。表記上普通は「is true」を省略していますけろ。
てか、こういうところが俺ちゃんタイプの文系ちゃんからすると(なんで暗黙のナニソレ的に説明省いてくれちゃんてんの?な感じで)超イライラポイントなんすけど、大多数の人々には気になんないんすかね。ないんですね、すんまそん(汗)。
ところで「true」または「false」のどちらか一方である真理値を持つstatementは「命題(proposition)」と呼ばれます。そしてP(x)は「xはP(=xは八角形である)」というstatementというか文であり真理値を持つので命題です。同様のことがQ(x)やR(x)についても言えます。
このとき命題「xはP」の変項xを「主語(subject)」、Pを「述語(predicate)」とみなします(上の例でいうと、変項xがsubjectなのは同じで、predicateは「は八角形である」かな?←そこはハッキリしようよ!←助詞の扱いとかアレなんだよ!:滝汗)。真理値は命題文に関して問われるわけですが、その文を二つの部品からなる構造に分けて(記号化して)記述できる所が特徴のようです。
そんなこんな(←?)で、このタイプの論理を「述語論理」と呼ぶのだとか。
「量化子(quantifier)」には二種類あって「すべてのxについて...(for all x ...)」と「...であるxが存在する(there exists x such that ...)」みたいなことを表します。前者を全称記号、後者を存在記号などともいうそうです。
さて、命題文を一塊で扱う所謂「命題論理」では量化子は使わないのですが、複数の部品に分ける述語論理では必要になってきます。大抵の論理の解説書みたいなのにも「述語論理では量化子を使う」旨の事務的(?)な断り書きは必ずあるのですが、例によってアレな俺ちゃんには(理由とか必然性とか諸々が)ピンとはきませんでした。そんで取り残されているうちにすぐ「ドモルガンの法則で量化子は...」みたいな話に進んでしまうま。
弁当箱はアルミ製です。
で、それについて考えるのに上記の文を使ってコネコネしてみます(ちな「アルマイト」はアルミニウムの耐食性を向上させるために加工して作られた皮膜のことらしいので「アルマイト製」というのは「アルマイト加工されたアルミニウム製」の省略形っぽいです...)。
日常会話などの実際の使用局面と異なり「弁当箱はアルミ製です」を他の文脈から全く切り離して(この文だけしか存在しないものと)考えたとき、このままでは情報が不足していて命題文としては曖昧なものと断ぜざるを得ません。つまりtrueかfalseか判断がつかなくなってしまうのです。
その原因は主に変項x、つまりsubjectにあります。
「xはP」の変項xがここでは「弁当箱」です。「いやいや弁当箱は弁当箱やろなんで変項になんねん!」と思うかもしれませんが、「弁当箱」とだけ言った場合、これは大枠を決めた(?)に過ぎず、何か「弁当箱」と呼ばれるものたちの集合をボンヤリと指しているだけなのです。そういう意味で変項xとなんら変わっていない。補足:「論理の箱庭」での変項xは9個のentityを要素とするuniverseに属していました。変項「弁当箱」も同様に弁当箱universeというかdomainに属するentityを要素とする全体集合的な何か...みたいな理解でいいんですかね?←質問か!
日常会話では文脈があるのでそれを利用して「弁当箱」が具体的に指し示すものを理解できるのですが、この文しか存在しない、という条件ではこのように考えざるを得ないわけです。
それはさておき、この命題くずれから曖昧性を取り除いてちゃんとした命題に仕立て直す方法はいくつか考えられます。
ひとつは「弁当箱」を具体的なものにしてしまうことです。つまり変項「弁当箱」ではなく「弁当箱」に含まれるひとつの定項を取り出してそれに決定してしまいます。
『スタンリーのお弁当箱』で主人公が持参した弁当箱はアルミ製です。
これなら(主人公が持ってきた弁当箱は一種類なので)命題としては確実にtrueかfalseかが決まるはずです。
>> Stanley Ka Dabba First Look Trailer
タイトルにあるワケワカラン文字列「Ka Dabba」はヒンディー語みたいです。上記trailerの最後に問題の「dabba(=弁当箱?)」が映ります(なんか金属っぽいのは確かですがアルミなのかは知りませんけろ←!)。
上記でひとつの定項に限定したのと逆に、いっそありとあらゆる「弁当箱」についての話にしてしまう、という手も考えられます。
すべての弁当箱はアルミ製です。
これも真偽は判断できます。アルミ以外の材質で出来た「弁当箱」が存在しますから真理値はfalseです。論理式では全称記号を使って変項をbindするタイプがこれに該当します。補足:変項とか変数というのはいずれもvariableで両者の区別は日本語固有の問題です。あとで出てくる「引数(argument)」もそうですが扱う対象は数に限定されないのにこんな術語に訳されているので混乱してしまいます。主語と述語もsubjectやpredicateとそもそも意味や用法の上で違ってしまっているし、関数っていうのも...とやっていくとキリがないので話を戻します(滝汗)。えーと、量化子でbind(=束縛?)されたものをbound variableといいます。ただの「弁当箱」だとbindされていないのでfree variableです。変項がfreeだとそれについての命題が成り立たない、というあたりのアレコレについては後に英語との兼ね合いで触れるかもしれないしほっとくかもしれない...←無責任か!
あああああああーっ!まちがえた!!
すべての弁当箱について弁当箱はアルミ製です。
日本語として「?」な文ですが「弁当箱」をあくまで変項として考えると、こう書かざるを得ません。そしてこれが意味するところは「すべての弁当箱はアルミ製です」ではなく「すべての弁当箱のうちアルミ製である弁当箱(の集合)」です。アルミじゃない弁当箱だとfalseで、アルミだとtrueになる...という感じかな?(←また質問か!)
ところで、最初に間違って書いた「すべての弁当箱はアルミ製です」という命題を表現するにはどうすればいいのでしょうか。おそらく変項xをsubjectとして以下のように書かねばならないのではないかと。
すべてのxについて「xは弁当箱である」ならば「xはアルミ製である」
「弁当箱である」という性質を持つentityの全集合が「アルミ製である」という性質を持つ集合の部分集合である、ということです。むむむ。
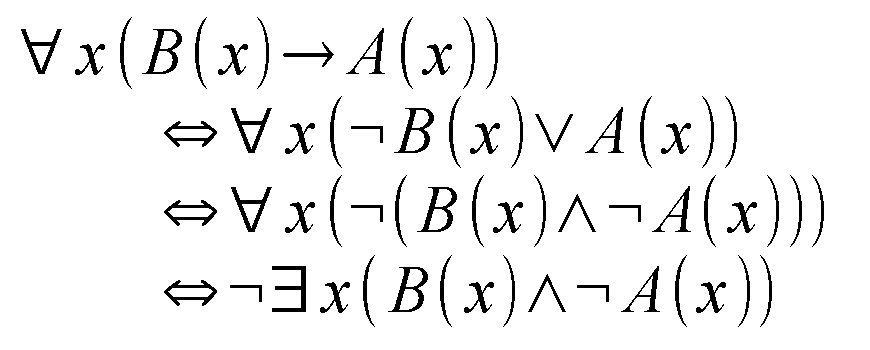
論理式で記述してみました。B(x)は「xはBento-bako」、A(x)は「xはAluminium」の意です(笑?)。一番上にあるのは命題をそのまま式に直したもの。二つ目と三つ目はそれぞれ最上段の式と同値である言い換えです。全称記号のスコープに入っている論理式に否定がついている(←こういう書き方でいいのだろうか...:汗)ものは、全称記号を否定のついた存在記号に変換した上で、その論理式についた否定を消す、ということができます。
その結果である四番目の式はザックリいえば「弁当箱であって、かつアルミ製でないxは存在しない」という意味の言い換えです。
えー、色々混乱してまいりましたが、「弁当箱」をbindするのに全称タイプがあるということは当然、論理式で存在記号を使うタイプも考えられます。
ある弁当箱について弁当箱はアルミ製です。
「いくつかの弁当箱について弁当箱はアルミ製です」とも言えるかも。いずれにせよアルミ製の「弁当箱」というものが存在するかどうか、という話ですから当然trueと判断できます。
あるxについて「xは弁当箱である」ならば「xはアルミ製である」
変項xをsubjectとする場合でもこのケースでは同じ意味になるような気がします。「アルミ製である」集合に「弁当箱である」集合の要素が含まれている、つまり両方の集合がちょっとは重なっている、ということを意味しています。
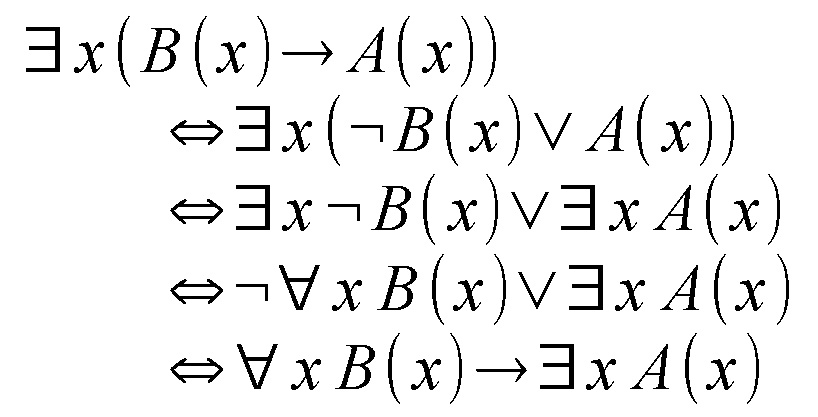
これも論理式にしてみました。全称記号のときと同じく最上段は命題をそのまま写したもの。二番目は「ならば」の言い換え。そして三番目なのですが、存在記号は「or」に関して分配法則が使えることを利用しています。ちなみに全称記号は「and」に関して分配法則が成り立ちます。四番目はその結果を踏まえつつ全称記号と存在記号の変換規則を利用しています。
この過程を経た結果、最後の式「すべてのxについてxが弁当箱であるならば、アルミ製であるxが存在する」に変換されています。「弁当箱というものの中には、アルミ製のものも存在するんだよ」的な意味でしょうか。うーん...論理式上のニュアンスの違いがうまく自然言語に訳せません。それはともかく量化子がbindする範囲(scope)が変わっている点がアレかと。
なんつか、日本語(英語は若干マシらしい感触はあるものの、俺ちゃんの英語力ではニントモカントモ...:笑?)に限らず、自然言語で論理式の意味するところを解説したり、逆に自然言語で言いたいことを論理式にしたりすることの間には相当な障害があるように感じます。
述語論理を扱うのに最低限必要な道具が一応揃った気配がするので、ここらで例の「三段論法」をもう一度引っ張り出してみましょう。
ソクラテスは人間である。
人間は死ぬ。
故に、ソクラテスは死ぬ。
「ソクラテスは人間である」という命題での「ソクラテス」は「定数/定項(constant)」です。「人間」の方は性質のはずですがニントモカントモ。
Socrates is a man.
Socrates is a human.
Socrates is human.
英語だと「人間である」のところで若干見解が割れています。人間集合の一要素というあたりをどう表現するか、の違いでしょうか。
「人間である」というのを性質H(humanからとりました、manからとってMにすると、あとで出てくるmortalと被るので...)としたときに、「a human」というのは(aはもともとoneで、スコットランドでは今でもoneはaneで、英語では語末のeは落ちやすいのでanになって、だからもともとaの方がanのnが落ちたもので云々)「one of H(x)」ですから、「Socrates is a human」とは定項「Socrates」が「すべてのxについてHという性質を持ったxを要素とする集合H(x)の一要素である」ということを言っています。
結果どうなるかというとH(x=Socrates)みたいな感じかと。これはhumanを形容詞として考えた場合でも同様に「SocratesはH」ということでH(Socrates)になります。
次の「人間は死ぬ」ですが、英語では大体以下のように言ってるみたいです。mortalは日本語にはピッタリくる訳語はない気がします。日本語では動詞になっちゃってますしおすし。「Every human dies.」は普通にある言い回しのようですがこの三段論法の文脈では使われていないような...。
All men are mortal.
All humans are mortal.
Every human is mortal.
Human is Mortal.
最後のものは日本人の著書にあった事例で、文中なのにmortalではなくMortalという表記ですから何か特殊な約束事の文脈があったのではないかと。allを使っているのはH(x)の全体を指しており、everyはH(x)のそれぞれの要素に着目しているということでしょう。
面倒なので端折りますが「すべてのxについてH(x)ならばM(x)だ」つまり「人間集合は死ぬもの集合の部分集合だ」という命題だと理解できます。
ここでx=SocratesによりM(x=Socrates)となります。
Socrates is mortal.
どうも自然言語で「fooはbaaである」というとき論理的な解釈が「B(foo)」だったり「F(x)→B(x)」だったりと異なる場合があることがわかってきました。命題においてsubjectの位置にあるものが、それ自身命題であるのか、それとも単なる(?)entityとしての変項であるのか、というあたりが関係してそうです。
またまたパワー不足や...。

ダメな文法理論とそうでないものとの差が「メモリつき句構造文法」やNK(エヌカー)で扱えるような階層構造を想定しているかどうかにある、という主張は生成文法派と時枝文法派(?)に共通していました。そして彼らは「前から順につなげていく」という考え方の言語モデル(=マルコフ連鎖モデル)を否定します。
こうしたことを考えていくに際して幾つかの(今までより更に:笑?)基本的な概念についてお浚いしておいた方がいいんじゃないかしらん、と思わなくも無い。どこまでも遡っていってキリがないのですが、これもまた文系ちゃんの宿命...。
「学問をするものは、近道をしようとしてはいけません。その学問のいちばん古いことからはじめることです。」ある人にそういわれると、轍次は、またぎゃくもどりして、古代中国の民謡や祭りの歌を集めた『詩経』といういちばん古い詩集の研究にとりかかることにした(p.33)
引用は『ことばの海へ雲にのって』から。「轍次」は『諸橋大漢和』でおなじみの諸橋轍次先生です。以下別の箇所からも引用。
「学問は、基礎さえしっかり固めておけば、今にどのようなことでもできるものですよ。」陳宝※(※は王偏に深の右側:汗)が、轍次に語った。轍次は、日本でもだれかにおなじことを教えられ、自分がそれを守ってきたことにあらためて思いいたった。(p.44)
相変わらずUnicode対応してなくてアレなんですが...(←RSSではUTF8で吐き出してるんだからすぐできるだろ!やれよ!←なんか宗教上?の理由で気乗りしないんじゃよ...)。
古いとこまで戻って基礎を固めてばっかいると、なんつか、取り残されちゃって生存そのものが脅かされるっす...という現実は子ども向け書籍には書いてなかったんすけろ。しかしなかなか習い性は変えられるものでもないんでアレですけろけろ。
そんなわけで(?)これからヨタヨタと書いていくのですが、文系ちゃんである私の理解(wikipedia風にいうと独自研究)ですんで、まあ間違ってたり無駄なことやってたりすると思うんですけど、思考パターンの似た人にとってはそれなりにお役立ちかもしれません。そこんとこは期待したい。
で、まずは「論理」の初歩からです。
「ソクラテスは人間である」「人間は死ぬ」故に「ソクラテスは死ぬ」という三段論法は(物理的には?)「五百円玉はサイフに入っている」「サイフはカバンに入っている」故に「五百円玉はカバンに入っている」と推論するのによく似ています。ときどき目にする雑な説明(?)に、「A=B」「B=C」故に「A=C」というのがありますが、こういうのはひどく誤解させるのでよくありません(特殊なケースとしてそうなることはありますけろ:汗)。
「AはBである」をもうちょっと論理っぽい言い方にした「AならばBである(例:ソクラテスならば人間である)」とは「AとBは等しい(例:ソクラテスと人間は等しい)」ではなく「AはBに含まれる(例:ソクラテスは人間に含まれる)」という意味です。
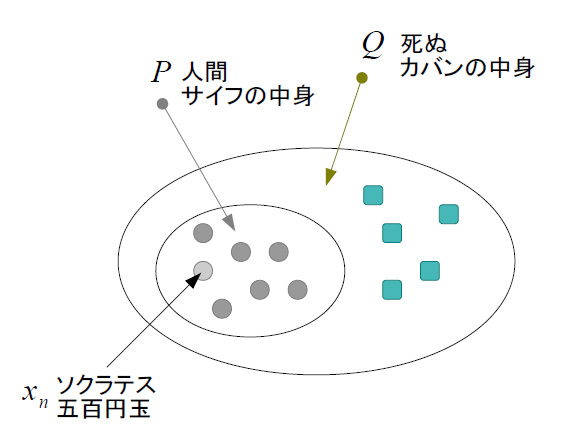
ソクラテスと五百円玉は何か個体というか実体であって「ある性質をもったカテゴリ」とは区別されます。たとえ話で言及した五百円玉が入っているサイフは実体なのですが、それについては「入れ物」性にのみ着目しています。「お金に関するもの」という性質をもったカテゴリ的な何か、ということです。
一方、「人間である」という性質をもったカテゴリ、というのは直接的には実体ではあり得ません。しかし、この集合の性質をPとして要素をxとした場合、集合そのものはP(x)と書けます(別にA(a)でも何でもいいのでしょうが、なんとなく...)。このとき「ソクラテス」は「x_1」(←xの右下に1)だとか「x_ソクラテス」みたいな「xのうち特定されたひとつのもの」ということです。
要素xがx_ソクラテスのようなもの{x_1,x_2,x_3,...,x_n}から成り立っているとすると、その集合には実体があるようなことになります。サイフそのものが無くなってもサイフに入っていたお金(五百円玉なども含む)集合があれば、それは実体を持った一塊といえなくはないみたいな。
このあたりのことは「内包(intension)」と「外延(extension)」という概念に関係します。この例では集合P(x)のうちPが内包でxが外延です。訳語から受ける印象だと何か逆な気がしますけろ(個人の感想です)。
不定形の何かがサイフ(=要素がお金という性質を持つ集合)に突っ込まれると各々が「お金である」という性質(?)を与えられて何らかの硬貨や紙幣として存在するようになる、というのは内包的(?)な解釈と言えそうです。一方、内容物を確認してみたら硬貨や紙幣ばかりだった、ということから要素の集合に共通する性質が「お金である」と認める、という順だと外延的解釈なのかな、と。
ものすごく素朴で単純なものを例示して色々確認していこうと思います。
まず「全体集合U」の四角い枠を書き、それからそこに「変数(変項)x」を散らします。簡単のためxは9個だけ。これらは「何の特徴もないが存在するもの」です(「特徴がない」という特徴があるじゃないか!←ウゼエ)。無性質という特徴を絵にするのがアレなので、なんとなく雲っぽい図(cloud nine...)にしてみました。
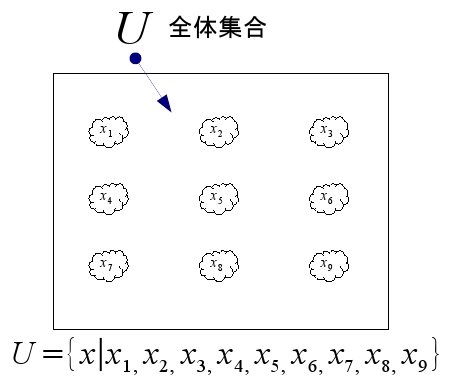
無個性といいつつアレですが、個々の識別はできないと後で色々言及していくのに不便なので、各要素に名前(?)をつけておきます。固有名みたいなもんです。
それと図の下につけた式でxの後ろにある縦棒記号(←!)は「定義する」という意味で使っています。変項xをx_1,x_2,...,x_9と定義する、みたいな。この記号を(2|n)で「nは2で割り切れる」のような意味(=「割り切れる」)で使うこともあるようです、為念。(→参照:『数学は言葉』(新井紀子、2009)のpp.65-67等々)
次に「P(=八角形である)」「Q(=色がついている)」という二種類の性質を持った集合を内包的(?)に作成してみます。これらの集合には重なり合う部分があり、そこに含まれる要素は両方の性質を兼ね備えます。

こんな感じです。楕円と重なった要素が性質を付与されて変化しています。もし最初に配置されたときから八角形だったり色が付いていたりする要素がこんな風に並んでいたのだとしたら、そういう特徴をもとにグループ分けをする中で集合が形成されていくことになります。これだとたぶん外延的(?)に解釈されたことになるんでしょう。
ま、いずれにせよ出来あがりは同じになります。さて、この図から読み取れることをいくつか「論理式」で表します。
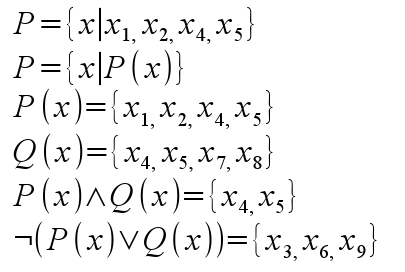
上から三つ目までの式は結果的に(?)同じことを表しています。小文字を要素そのものというモノ的な何かを表すのに使い、コト的な性質を現すときには大文字を使うという方針を徹底するのであれば、P(x)はp(x)と書くべきかもしれません。
この素朴な「箱庭」の例では(固有名までバッチリ!で)実体であることが実感できる要素が使われているため、性質的なものとの差は歴然です。しかし要素数が無限であり、しかも離散的ではない(=自然数の集合と一対一対応不可能な)要素を持つ集合を扱う際などにはこの区別は自明とはいえなくなってきます。
そういうアレコレも考慮して(?)ここはp(x)ではなくP(x)でいきます(なんか論理の話をしているのに支離滅裂な説明...←うるへー!)。
式の説明に戻ります(汗)。
四つ目の式は性質Qを持ったxの集合を表しています。その次はP(x)とQ(x)の重なっている部分の集合です。論理結合子「かつ(and)」を使っています。これって呼び名がandなのに振る舞いが乗算的なのでイヤンな感じ。
最後の式で使われているのは論理結合子「非(not)」と「または(or)」です。orは加算的に機能します。P(x)とQ(x)の要素を足した(でも共通部分の要素を二重に加えたりはしない)集合に「非=ではない=それ以外」を付けていますので、結果的にですが、図の右端列に放置されていた三要素に「八角形でもないし色もついていない」という性質を付与(?)した格好になっています。
ところで下から四つ分の式では、変項xの具体的内容がすべて異なっているのですが、こういうのを普通の人々はスンナリ飲み込めるもんなんでしょうか。てか、もんなんでしょうね、間違いなく。
たとえば下から二つ目の左辺をR={x|八角形で色つき}つまりR(x)に置き換えて表現します。これでP(x)やQ(x)と同じような表記になるわけですけろ、この三つの集合でxの示す具体的な意味(「要素である何か」という抽象的っぽい意味はそのままだけど:汗)は一致してないわけです。うーん、当然なのはわかるんだけど、なんかムズムズする感じ。
こうした「変数(変項)x」という概念への違和みたいなものについては追々書いていくこととして、とりあえず先に進めます。
えーと、論理に必須の「論理結合子(connective)」は全部で七種類あって、上で三つ出ましたので残りは四つ。未言及の内訳は「ならば(then)」および双方向「ならば」である「同値(if and only if equivalent)」、それに「量化子(quantifier)」二種類です。量化子に関しては変項x問題が大直撃することになるんで面倒くさすぎることもあり、後回しにせざるを得ない...。
「AならばBである」は集合論で言い換えると「AはBの部分集合である」になります。これについては五百円玉やソクラテスの例でもすでに言及しました。
「AはBの部分集合である」とは「集合Aの要素であって集合Bの要素でないものはない」と言い換えられます。もうちょっと論理式に寄せると...(「集合Aの要素」「かつ」(「集合Bの要素」「ではない」))「ではない」...とも言える(笑?)。
このくらいまでなら論理式を使わなくても楽勝でしょう。しかしこれと「集合Aの要素ではない、あるいは集合Bの要素である」が同じことだと言われたら「はぁ?」となるのではないでしょうか(実際、今これを書いていても不安になってくる:笑?)。
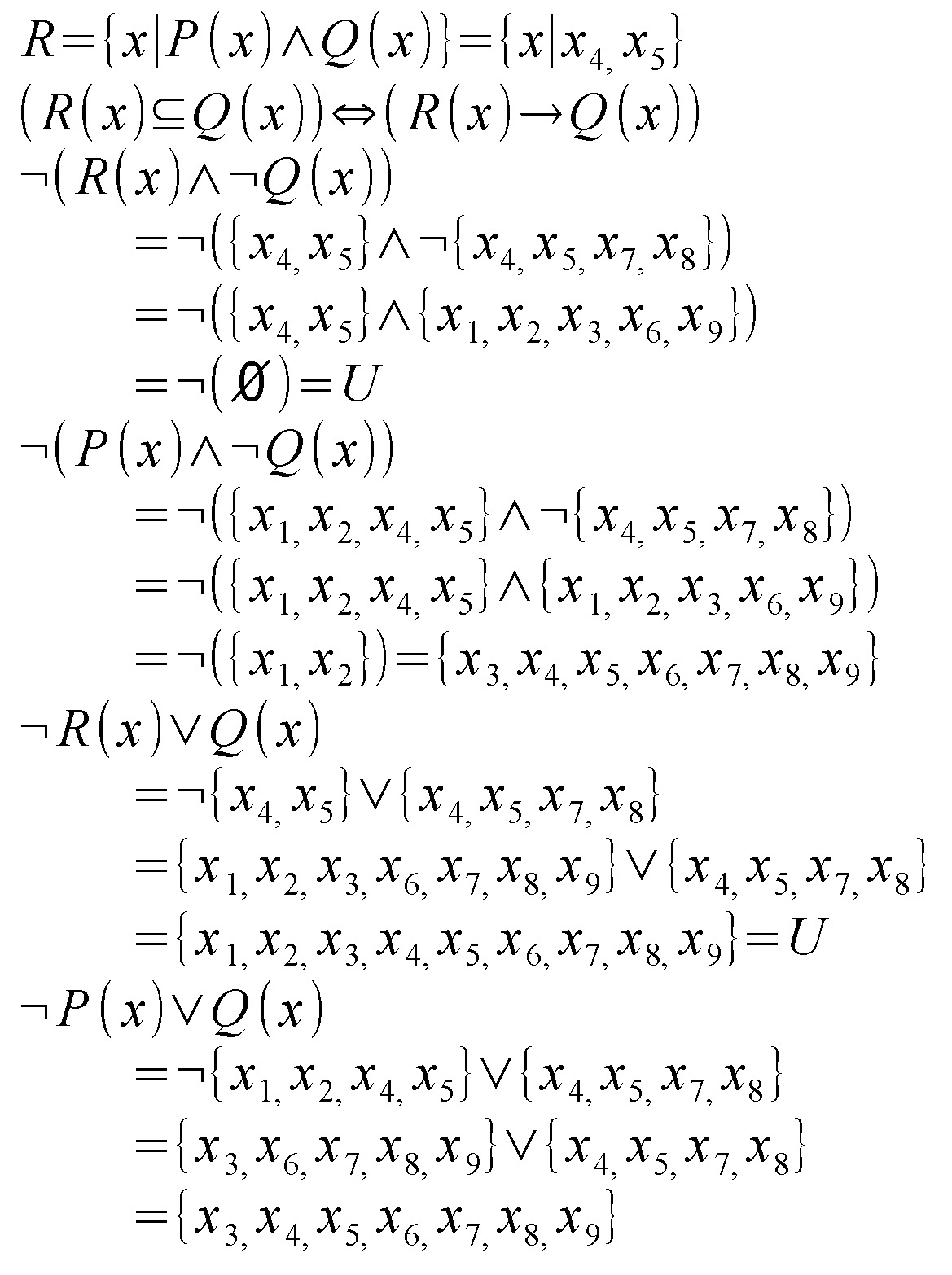
最初の行は「箱庭」のP(x)とQ(x)が重なる部分をR(x)として定義し直しています。次の行では集合論の記号で「R(x)はQ(x)の部分集合である」と表現したものと、「ならば」記号を使ったものを「同値」記号で結んで示しました。
三行目からは、実際にQ(x)の部分集合であるR(x)と、そうではないP(x)の双方を用いて、二種類の論理式を使った結果を検証しています。この二種類は「集合Aの要素であって集合Bの要素でないものはない」と「集合Aの要素ではない、あるいは集合Bの要素である」をそれぞれ論理式化したものです。
R(x)の場合はどちらも全体集合Uになり、P(x)では全体集合からx_1,x_2(=P(x)とQ(x)が重なっていない部分)を欠いたものになりました。論理式は一見すると相違してしますし演算過程も異なるのですが、「重ならない部分」が存在すると演算結果が全体集合にならない、という同じ仕組みだったようです。
ま、いずれにせよ「ならば」記号は「かつ」「または」「非」で置き換え可能と確認できました。そんな感じで(←!)。
パワー不足や...論理の初歩の最初のステップくらいしか書けんやった...(涙)。

ちょっと趣向を変えて『曲がり角の日本語』(水谷静夫、2011)に言及しつつ生成文法派や句構造文法について考えて見ます。
まず非常に素朴なところから、日本語の文というのはどういう仕組みをしているかから考え直す必要があるだろうと思います。実は、チョムスキーは、文が文法論で扱う極大の単位だと説きました。文法というのはその極大の単位である文の構造がどうなっているかを調べる学問分野だと言っています。ちなみにチョムスキーは「極大」ではなく「最大」という言葉を使っていますが、彼は世評と違って数学が意外にもできない男ですから、最大と極大との区別を知らなかったようです。(p.109)
(チョムスキーよりオレの方が賢くて偉い、とおっしゃりたいのかしら?という以外は)全くわからん...(滝汗)。「最大」っていうのは単に「形態素」「語」「句」などに比べて大きな(長い?)単位であることを指していっているだけだと思ってました。それ以上大きな単位、たとえば「段落」などというものは文法的な単位とはいえないだろう...というのはとりあえず誰しもが納得するのではないかと。
しかし「最大」ではなく「極大」が正しいと書いてます。チョムスキーが「世評と違って数学が意外にもできない男」であるため「最大」と「極大」の区別ができていないと断じているんですけど「特に意外でもなく数学ができない男」(←!)であるオイラには全く意味がわかりませぬ(涙)。
「極大」というのはmaximalのことで、数学用語として意味を限定すると「極大値」のことだと思われます(対義語はminimalで「極小」または「極小値」)。日常語としてなら「極大」も「最大」も大して違いはないでしょうが、数学用語としての「極大値」と「最大値」なら確かに違ったものを指しますので両者は区別されなくてはなりません。それはわかります。
極大値も極小値も、グラフが増加から減少(または減少から増加)にシフトする点を指していることに注目しましょう。f'(x)の正負が変更するポイントが極大値、極小値であるとも言えます。
高校数学の範囲ですが文系ちゃんでも教わるレベルかと。定義域(上の例だとxの範囲)によっては極大値と最大値が一致することもありますが、そういう場合を除けば(上の例だと)xの値がずーっと右の方(←!)に行けば行くほど、それに対応したf(x)の値はどこまでも大きくなる関係です。
x=aの近くで関数f(x)が連続で、f(a)が最大となるとき、f(x)はx=aで極大であるといい、f(a)を極大値といいます。(p.87)
引用は『家庭の算数・数学百科』の「極大値」から。「近くで」というのがずいぶんアバウトな話に見えますが、まあ、同じようなことを言うてはります。
さて、「極大(値)」と「最大(値)」の数学における区別については確認できたのですが、「文が文法論で扱う(最大の、ではなく)極大の単位だ」という話とどう繋がるのかは依然として(仮に比喩だとしても:汗)「?」です。
すぐには答えがでそうにないので、とりあえずこの件は保留しておきます...。
水谷(2011)を読み進めます。
実は論理学にNKと呼ばれている論理体系があります。木はその証明図と本質的に同じ構造である事が知られております。証明したいことにたどり着くために証明図は、既知の条件を梢にずっと並べるわけです。それから、許される論理の図式を使って、順々に形を書き替えていきます。そして最後に目指す構文カテゴリ、ここでは文に帰着できれば、構文解析が完了ということになります。ですから、先のような構文図を描いて構文の木を作ることは、論理学的な証明図を構文に関して作っているのと同じことなんです。めでたし、めでたし。(p.123)
「先のような構文図を描いて構文の木を作る」というのは例文「酷いじゃない」を「酷い」「じゃない」に分けて、順に「述素*」と「【述】」に置き換えて(末尾に「【結び】」を加えて)から、両者をあわせて「述態句」に、そして最終的に残った「【結び】」とセットで「文」にする...みたいな事例を四つあげてあることを指しています。要するに構文木です。
非終端記号の種類や書き替え規則が独自のものであること、および上部に文があって下に書き足していく、というのも生成文法でのtreeと異なっています(木のはずなのに枝を下に描くなんて、的な感じで「チョムスキーは比喩の使い方が下手だと思います」とここでもdis...)。
話は前後しますけど、冒頭付近に出てくる「NK」は引用元では「エヌカー」とルビが振ってあることからもわかるように「Natüriche Kalküel」というドイツ語の略です。これは英語圏でいう「Natural Deduction(自然演繹)」のことで、何やら(ラッセルやホワイトヘッドとは)別系統の論理学なんだとか。パッと見た感じの印象の違い以外の差異はよくわかりませんけろ(←雑か!)。
Historical. Original ideas of Gentzen, who in [109] introduces two systems: NK(Natüriche Kalküel) and LK(Logistiche Kalküel). The former is just ND system, whereas the latter, which is a sequent calculus, is meant as a technical tool to prove some metatheorems on NK, not as a kind of ND.(p.31)
引用は『Natural Deduction, Hybrid Systems and Modal Logics』(Indrzejczak, A.:2010)から。なお[109]は以下の論文を指します。
>> Gentzen, G.:1935,Untersuchungen über das logische Schließen
NKはNDだけどLKはNDじゃない、みたいな感じかな。テキトーですが。NKがNDなら問題ないからいいですよね、どうでも(←投げやりか!)。
>> NK演繹図(ひとしきりのひとりごち)
上記引用サイトにわかりやすく基本的なことが手短に(←超重要)整理されているので参考になるかと。ありがとう&幸あれ。
ええと、水谷(2011)では「記号列が規則の適用によって置き換わりながら減っていく過程を途中で横線を引きながら書き綴っていく」点を見て「本質的に同じ構造」と言っているようです。
「酷いじゃない」という例文での「酷い」「じゃない」という記号の並びをNKでの「A B」という二つの命題の並びと同じに扱う(ちな横線下は推論によって「AかつB」になります、なお「かつ」は論理結合子を使うべきですがアレなんで:汗)のが間違っている、とは(たぶん?)いえません。NKでは推論を重ねた先で必ずひとつの命題だけが導き出されますが、それも最終的に「文」または「S」というひとつの非終端記号へと導かれる構文解析結果と似ています。
「帰納的or再帰的に可算(recursively enumerable)」であることを解析して示すことは、推論が論理学的に正しいことを証明する行為の一種であって「論理学的な証明図を構文に関して作っているのと同じこと」でしょう。うんうん、確かにそう。ある記号列が特定の(再帰的に可算な言語の)文法によって生成されたものであれば、その文法の規則を用いて論理的に解析可能である、という例の話です。
ですから「NK演繹図を用いて様々な事例を論理学的に正しい推論であると証明してきた」こととの相違点は(この話題は以前にも触れましたけろ:汗)自然言語に関してそういう規則集を実際に作れた事例が存在しない、という点ですね...(笑?)。
読み進めます。
ところで先の構文図には、ある段階の述素の末部に直前の段階の述素が入っている---つまり述素の入子が、幾つもありました。図1のは簡単な構造のしか扱っていませんので、他の種類の入子が現れませんけれど、もっと複雑な構文の場合には、体言から出発した体言性連語の入子とか、あるいはまた述態句の入子とかいったものまであります。このように、ある構造の中に同じカテゴリをはめ込んだ仕組みが<入子構造>なんです。この事あって、有限個の規則でもって、無限に多い表現を律することができます。(p.124)
先に挙げた例文「酷いじゃない」には入子構造はありません。図1にあった別の例文「美千隆も猜疑心が強い?」にはあります。「強い」が最初の段階での述素であり、「猜疑心」「が」と一緒になって「猜疑心が強い」という述素になるのだとか。さらに「美千隆」「も」とで述素を作る、という具合(なお、書かれていない「零記号」の「述態辞」とこれとで述態句、「【結び】」である「?」と述態句で文が出来る、ということのようです:汗)。
ぼんやりと読むと「述素」の話は生成文法理論(GB理論時代?)でいう「Xバー理論」っぽい話に見えます。Xバー理論もアレコレ弄られすぎて何がなんだかわからない感じになってる上にすでに棄却されているので、それに似てるとか似てないとか言ってもアレなんですけろ。
このように日本語には述態文と喚態文とがあると、私は考えます。研究者の立場では、与えられて解析する一番長い範囲、つまり、極大述素の後に、【結び】が付いた場合に述態句になります。(p.130)
ここでいう「極大述素」はXバー理論の「最大投射範疇(maximal projection)」と似ているようでもあります。てか「maximal」いうてますね。「文」に関しては「the largest structural unit」だから普通に「最大」やと思いますが。為念。
それと「極大述素」が(入子となっている述素と同じように零記号を含む何らかの「述態辞」と一緒になって)「述態句」になって、これに「【結び】」が付いて「述態文」になるという話なんじゃないかな?本来は。この箇所は他の説明部分と整合が取れてない気がします。
句と文とはきちんと区別しなければいけません。意味論的に非常に重要なところです。その区別をきちんとしないから、文法がおかしくなるんです。隈付き括弧【 】で書いたものは、すべて文法上のある働きを抽象化して扱う時、それに名称を与えたものと考えています。述態句の後に【結び】が付くと(述態)文が成立する。荒っぽく言うと、述態句の範囲では何か述べていますけれども、自分の強い主張というのはまだそこには出ていないのです。結ぶことによって、自分はこう考えているという態度を押し出したわけです。喚態文の所でもう一度述べますが、句と文とは異なる概念です。(p.120)
少し戻って引用しましたが、上記のように「述態句の後に【結び】が付くと(述態)文が成立する」と言っています。「【結び】」は「。」「?」だとか本来それらが入るはずだが省略されている場所に置き換えられる非終端記号のことらしいので「文」の途中複数箇所に使われることはないようです。
うーんと、ここで唐突に最初に保留しておいた「極大」の話に戻ります(←!)。
水谷(2011)では(述素からなる)無限の入子を可能性として持つ構造のうち、一番大きなものを「極大述素」と呼んで、これが句になるとしています。そして文はこの句を下位範疇とする構造です(両者の実質的違いはpunctuation markを含むかどうか)。
あくまでたとえというかイメージというか比喩的なものなんですけど、これって等比数列で公比が1より小さいときに無限級数が収束する、つまり級数の和=「極限(limit)」みたいなことが言いたいのかなあ、的な。そんな気がする程度の話ですけろ(←正直飽きてきた←しっかりやれよ!)。
上述した「入子構造」を取り入れた理論であるかどうかで文法理論の優劣を判定できるとしています。
入子の考え方を文法論に初めて導入したのは、私の師匠である時枝誠記です。昭和九年(一九三四)の事でした。当時は、若干の記号論理学者がこれに気づいていたとしても、西洋の言語学者はまだ誰も、近代言語に備わる入子構造も入子の効用も知るに至っておりません。(略)時枝文法論の中核は入子構造に存します。
私に言わせれば、入子をきちんと使うことができるかできないかが、新しい文法理論と古い文法理論との境目になります。そういう面で言いますと、学校文法の基を成す橋本文法説には入子の考え方がありません。橋本進吉が亡くなるちょっと前に書いて遺稿となったものに、「連文節」という言葉が使ってあります。あれを入子と考えれば考えられなくもない。いくつかの文節が連なって、一個の文節のような働きをすることに対して、橋本は「連文節」の名を与えました。まさに竹の節のように連なるだけのものであって、入子の構造をそこに見たわけではありません。文節的構造論は弱体です。(pp.124-125)
ダメ理論の例として「学校文法の基を成す橋本文法説」を挙げています。入子構造に対応していない「文節的構造論」である点が劣るという評価です。
ただ『国語学原論』(時枝誠記、1941)を読みますと(岩波文庫版では下巻の冒頭からが入子構造の文法論に関する記述になっています)橋本文法を対立するものとして批判している感じもありません。特に穏やかな言い回しを選択するタイプの先生でもないようですし、全否定する気がそもそもなかったんじゃないでしょうか。
むしろ「國語に於ける表現形式を、以上の様に考えて来る時、ここに始めて橋本博士の文節論と、文章法的分解との間の矛盾を克服する道が開けて来るのである。」(p.319、時枝1941)(岩波文庫版下巻だとp.17)というようにアウフヘーベン(?)してます。両者の間に断絶はありません。
そもそも「文節」は主に二語から成る単位ですので、ただ単語を前から順に繋げているだけ...と考えるモデルではなく、「S→文節」および「文節→自立語+付属語」(もちろん「自立語→{自立語の集合}」「付属語→{付属語の集合}」云々といったアレコレも必要ですけろ...:汗)という生成規則だけが適用された(質的には?)不完全かつ不十分なツリー構造といえなくもありません。「文節の分解が、國語の分解に於いて極めて自然のものである」(同頁、時枝1941)とも言っており、時枝文法はこの文節という単位は必須のものだと認めたうえで、それらの関係性について新たな提案をしているのです。
時枝文法が一線を画そうとする対象は、たとえば下記のように説明されます。
S-Pの形式を以つて、思想表現の動かすべからざる原則の様に考えた結果が、従来文章法上で説かれた主語述語の関係であつたのである。今この伝統的な結合の観念を脱却し、統一といふことは、更に別の形式に於いても考へられるといふことを知る時、國語の表現形式は又別の意味に於いて理解されることとなるのである。(p.317、時枝1941)
「S-P」(←たぶんSubjectとPredicate)と「主語述語」を書き分けているのは「國語の構造は、決して主語述語の対立を、S-Pの形によつて統一する印欧語の如きものと同様に考へることは出来ないのである。」(p.316、時枝1941)とあるように前者を印欧語(およびそれに付随する言語学)での現象(?)を指すのに使っているからではないかと思われます。日本語には「詞」と「辞」があって(特に「辞」に)独特の役割があり、それによって(たぶん日本語=國語に独自の構造としての)「入子構造」が生じている、という考え方をしているのではないでしょうか。つまり、時枝文法の「入子構造」と生成文法派の「階層構造」はちょっと見た印象が似ているだけで、本質(!)的には全く相容れない別概念なんじゃないかと言いたいわけです(時枝誠記先生だけでなく山田孝雄先生の弟子でもある上にチョムスキーを数学の出来ないヤツとdisるほどの大先生がおっしゃることにケチつけるわけやね...ガクブル)。
このあたりのことは大変入り組んでいるので、また機会を改めて書いてみようと思います(←ちょっ!逃げんなや!!←いろいろあんねや...)。

チョムスキーの1956年の論文を読んでいるうちに「?」が巨大化したので色々別方面のことなどをアレコレやったりしていました。それでなんとなく「こういうことかな?」と思ったことなんかを書いてみます。
さて、あの論文の内容そのものは(優に半世紀以上未来である現在の観点から見れば)別に難解でもないのですが(小文字のエルと数字のイチが同じ印字とかいうタイプライター式表記だったりするのはめっちゃ難敵ですけろ:涙)何故マルコフ連鎖を使った言語モデルを全否定できたと断じちゃったのか、そしてその後もずーっとそういう主張をしてきたのか(過去5年以内でも相変わらずそういう主張をしています...後で触れると思いますが)は「?」です。
>> Chomsky, N.:1956, Three models for the description of language
Chomsky(1956)ではタイトルにもあるように三つの言語モデルについて書いていました。句構造文法(オートマトン)における区分は四つ(「有限状態オートマトン」「プッシュダウンオートマトン」「線形拘束オートマトン」「チューリングマシン」)ですから数が合いません。別の基準でモデルを選んでいます。
最初に言及されるのは「有限状態マルコフ過程」(自然言語の記号列は離散的なので「マルコフ連鎖」な気が...ま、とにかく「正則文法」の変種である「確率有限オートマトン」)です。これが自然言語のモデルとしてまったく不十分であるとして「句構造文法」(というか「文脈自由文法」)の優位性を説き、しかしそれすら極単純な文にしか対応できないという流れで(三つの言語モデルのうち)二つについて述べます。
現代の視点でいえばこれらはどちらも句構造文法の下位区分とされていて、両者を区別するのはメモリの有無です。正則文法にはメモリはなく、文脈自由文法にはあります。要するに文脈自由文法では計算(?)の順序がある程度変えられるけれど、正則文法では必ず前から順に処理しなければならないということです。
話を簡単にしてイメージしやすくするため電卓のたとえ話(?)をしてみます。メモリ機能のない電卓の場合「左から右(前から後)」という原則と異なる計算順序を持つ式には全く対処できません。1+2-3+4なら計算できても(1+2)*(3+4)は無理ということです(実際にはカッコ内を先に計算して結果を紙にメモって...とか脳内に記憶して...という方法で計算できますが、ここでは電卓のみで完結した計算をする話をしています:汗)。
一方、M系列(?)ボタンのある機種であれば「1,+,2,=,M+,3,+,4,=,*,MR,=」みたいにして(電卓にも依るし交換法則を使ってるけろけろ)計算できます。この種の電卓には数字一個を格納できるメモリ空間が装備されている、とみなして良いでしょう。物理的な空間でイメージすると鉄道の待避線(ただし一両分の長さしかない)みたいな感じ?
文脈自由文法ではこの待避線の長さが無限です。格納されているデータから取り出せる要素の位置が決まっている(=後入れ先出し)という制限はあるけどその分どんだけ長くてもオーケーみたいな特徴があります。「後入れ先出し(Last In First Out)」というのは「スタック(stack)」というデータ構造で、最後に入れた(?)ものを最初に取り出すという方式のことを言っています。
a data structure from which items are removed in the reverse order from which they were inserted; also called a pushdown stack or pushdown store.
上記は『Dictionary of Computer Terms』(Dowing,D.et al.,1995)におけるstackの説明冒頭の引用です。突っ込んだときと逆順でデータを取り出す的なことが書かれています。つまり「後入れ先出し」とは「入れるときは最後尾に付け足して、取り出すときは先頭から」を略したのではなく「後で入れたものから先に取り出していく」のことらしい。「名前(用語)なんてどうだっていい」という意識が透けてみえるというかなんというか。もう少し混乱しないようなアレ(たとえば昔のMacOSが「複製」と「コピー」を分けた気遣いみたいなの)があっても良いのではないかと。
また引用ではstackは別名「pushdown stack/store」であるとも言っています。文脈自由文法に対応したオートマトンは「プッシュダウンオートマトン」と呼ばれていましたが、どうやらこれは「pushdown stackを装備したオートマトン」という意味だったようです。なるー。
ところで自然言語を扱うときの計算(?)的な何かとは「書き換え規則(a.k.a.句構造規則、生成規則...)」で記号を置き換えることでした。そして文を作り出すときと逆の手続きで最終的に「S」という非終端記号に戻せれば(=解析できれば)ある文(=終端記号のみで構成された記号列)がその規則によって作られた、つまりその言語の文であると認定できるわけです。
この認定作業において、文を構成する終端記号を左から右に(前から後ろに)順番通り、最左端(最先端)付近の部位だけを対象に規則のリストから適合するものを選択して適用することで置き換えていって処理が済むのであれば、正則文法でもその言語(の文法)モデルとして十分だと言ってよいでしょう(...ですよね?)。
たとえば「英語の簡単な命令文の集合であるような言語」(軍隊とか単純労働で指示通り動くことを期待される人間やロボットへの一方的命令用言語とかとか)なら恐らくこれで記述できます。必ず先頭に動詞が来て、あとは目的語となる名詞か句動詞を作る副詞や前置詞が(順序は...予め固定して制限しておきますか:汗)並ぶ、とかとかを想定して置換規則等々を用意しておけば処理の順序は左から右(前から後ろ)だけでやっていけそうです。
けれどこれでは明らかに「自然言語」の記述は出来ていません。自然言語(=英語)のsubsetである人工言語を対象とした文法です。生成された文が英語として「も」読めるというだけで。というか、ちゃんとした英語っぽくしようとすると上記の簡単命令文人工言語でさえ書き換え規則は相当面倒くさいことになりそう。
あと繰り返しになりますが、学校で習ったような英文法での解釈を再現しようとするならやはり正則文法では無理だと結論するしかありません。たとえばkick the bucketを(kick the)bucketの順で処理するとか、あるいは三つの記号全部を一気に置換する(←例文は慣用句なので意味的にはこの方法が吉っぽいですが話がややこしくなるので...:汗)ような規則ではなく、kick(the bucket)の順で(常識的に?)解析するにはkickを一旦保留しておいてthe bucket部分を先に処理する必要があります。それが可能なのは文脈自由文法のようにメモリがあるものでなければならず、そんでもって具体的かつ一般的にはどう処理するかの説明はすっごく(どうやっても分量的にヤバイ的な感じで)大変なので、ここはひとつアレということで...(滝汗)。
・・・というようにグダグダ気の向くまま論じていると何を問題にしているのかが(読み手だけでなく書き手にも!)わからなくなってしまうので一旦話をぶったぎります。
Chomsky(1956)ではそれまでにも知られていた二つのモデルの欠点を踏まえた上で第三のモデルを提示しており、それが「変形生成文法」(←初期の生成文法理論)です。この理論では実際の言語使用において現れる「複雑で生成規則を適用し難くみえる文」と「生成規則で解析可能な文」を「変形規則」によって関連付けます。つまり句構造文法の自然言語への応用に際して、別系統の規則体系を併用する(=前処理に利用する)という点に生成文法派の独自性があった...みたいな。
一方、工学の自然言語処理分野では「変形規則」的な役割、つまり「文脈自由文法における生成規則数の抑制手段」として「素性構造(feature structure)」を利用したようです。時系列や影響関係はよく知らないのですが、生成文法理論が後に「変形規則」を捨てて「原理とパラメータ」などと言い出したのは「素性構造」のパク...じゃなくてインスパイアかな?などと思ったり思わなかったり。
生成文法派の初期(標準理論とかとか)から中期(GB理論とかとか)にかけては、色々なことが言われつつも基本的には(メモリのある)句構造文法をベースにアレコレいじっていた...ように見えます。つまりこの観点からみると一貫性は一応保持されていたといってもよいのかも。
また有限状態マルコフ過程モデルについても一貫して全拒否かつ全否定。表面的には階層構造を扱えない(「線的近接性(linear proximity)」だけを見て「構造的近接性(structural proximity)」を無視する)ことを理由にして批判しているようですが、本当の理由は別にあるんじゃないかと。「確率的言語モデル」への(生理的かつ宗教的?な)嫌悪が主因で、句構造云々は単なる誤魔化し(←実際理由になってないですしおすし...)に思えてなりません。
ところで、工学の自然言語処理では「隠れマルコフモデル」が形態素解析や品詞タグ付けなどに広く利用されており、また音声認識などでも非常に有効な統語解析手段になっています。こういう現実もあるんですけど、どうなんでしょう。
実は割と最新に近い生成文法理論では、初期から中期にかけての「句構造文法のなんらかの発展形」としてのあり方が否定されてしまったようです。以下引用は『チョムスキー言語基礎論集』(Chomsky,N.:2012)から。傍線は引用者が付けました。
The fact that IM and EM are both made available by what appears to be the simplest possible system of generation gives strong support to the idea that this elementary form of recursive generation is in fact the process incorporated in I-language, not some alternative that might be considered (e.g., axiom systems, or satisfaction of selectional relations, or reliance on some descendant of phrase structure grammar, etc.).(p.24)
IMは「内的併合(Internal Merge)」で、EMは「外的併合(External Merge)」だそうです(external mergeという術語はexternal sortingの代表的手法のこととして既存のものだったのに、こんな風に別の意味で使ってしまうとか、なんつか迷惑以外の何物でもない気が...:怒)。なにやら「the fact」が「the idea」に「strong support」を「gives」だということのようですけろ、こんな文(一文やで、これ!)でも苦も無くスラスラ読めて当たり前なモンなんでしょうか、人類ならば!!生得的言語能力で!!!
ちなみにこのカギカッコで示した部品(?)に「to」も加えてthe fact gives strong support to the ideaを生成したりするのがEMで、「the fact」と「that IM and EM are(...)system of generation」をつなげて引用冒頭の「gives」手前までのように生成する(?)ことをIMというようです。「the idea」と「that this elementary form...」以下文末までの関係も同じくIMかと。他にも部分的に見ていくと色々いえると思いますけろ。
簡単にいうと、EMがdistinctな関係、IMがone is contained in the otherな関係ということらしいです。そんで、このふたつだけでも再帰的な生成システムはつくれるっちゅーわけですね。だから(?)これこそが「I言語(I-language)」に組み入れられてるシステムであって、傍線部にあるような「句構造文法の末裔(?)」みたいなのを含むsome alternativeはアカンということをいってます。I言語は生成文法派にとっての言語(人間精神に内在するmental organとしての言語という意味での「内在化された言語(internalized language)」で、実際に行われる言語使用の総体としての「外在化された言語(externalized language)」に対立)のことなので、要するにこれまでの生成文法理論がやってきた具体的な取り組み内容のことは否定しちゃったっぽい(笑?)。
今までやってきたことを整理統合したら「elementary form of recursive generation」だけでよくなったと。つまり「再帰」だけが残った...みたいな。ま、確かにこういう流れ(?)で言っていることに対して「アマゾンの奥地に再帰が使われていない言語が実在するっ!だから生成文法は間違いだっ!!(ドヤァ)」って勝利宣言されたら当惑しますわな。そこんとこは同情します。
昨年あたりからずーっと生成文法周辺について言及しています。そんで久々に生成文法関連の昔の書籍などを読み返したり比較的最近書かれたものを確認したりしていました。直接的な興味は全くないのでひたすら苦行なんですけろ。
さて、ヤングだったころは生成文法なんて自分の人生とは全く関係がない、というか人類とほとんど無関係な理論だと思ってました(笑?)。実際に使われている言語=「E言語(externalized language)」と関係ない脳内限定(←!)理論だそうなので。まあ、勝手にやっててください的な。
単に個人的にそう思っていた、というだけでなく私が育った環境では(共通認識として)生成文法については(ちょっと半笑いで)「あーなんかやってるよねー」くらいの評価だったということです。なのでそれを常識だと思ってました。
ところが別の場所では「誰にも揺るがすことの出来ない真理」みたいな扱いになっててビックリドッキリですよ。定説だの真理だのいう以前に「場合によっては正しい...かな?」程度の部分を見つけるのにさえ苦労するようなシロモノだとしか思えませんが。
てか、今ここで長々書き連ねるのもアレなので自重しますけど、生成文法理論ていうのは理論構築に失敗しかしていない試みなんですからね?生成文法の歴史は失敗仮説の死屍累々ですよ?...何をもって「正しい」と思えるのか全く理解できん。どーかしてる。
むー、興奮しましたが話を戻します(←?)。
上記の評価ギャップに気づいたのは、思い起こせば十数年くらい前でした。語学教育関連で語用論に与する(?)方々が生成文法派帝国(←!)からの独立を目指して奮闘している姿を目にして驚いたのが最初じゃなかったかな。
彼ら(=語用論派)の手法に関して(「少ないデータで短絡しすぎ」「他の解釈可能性とか無視しすぎ」「反例いくらでも出せますけど?」程度の素朴な)批判意見を述べると、半ば自動的に「生成文法派に攻撃された」という想定のもとで(「精緻な文法理論の観点から見て本研究が不十分という指摘ですが、文法に基づいて分析をしても実際にはうまくいかないわけで、つまり文法に囚われるのではなく、一見場当たり的に見える談話分析とか会話分析の方が有用であって...云々」というような)明後日の方向に反論されて辟易するみたいな経験をしました。なんつか説明が下手でうまく伝わらないと思うのですけろ(滝汗)。
このとき「文法」とだけ彼らが呼んでたものが実際には「生成文法理論」のことだとわかるまで結構時間がかかりました。口頭でのアレコレだけじゃなく論文なんかでも単に「文法」を「生成文法理論」の略称に使ってて、でもその「文法」(a.k.a.生成文法)の具体的な姿はボンヤリしていて(つまりどの時代の生成文法理論のどういった具体的理論なり仮説なりについての話をしているのか)判然としませんでした。註:ゲス(=下衆+guess)パー能力で推察すると、生成文法理論ついて全くウロなままで言及してたんかなー、ってか、生成文法の影響を受けてる人たちが色々バージョン違いが混ざった状態でアレだからな...
英語ならまだしも日本語教育でこんなだったのは本当に衝撃でした(日本語教育研究者は大抵米国の大学で学位を取って英語の文献しか読まないし英語でしか研究を発表しないような方々ばっかりなので、まあ、それはそうか、という気もしないでもないような...)。日本語の「文法」といえば「日本語生成文法」(?)だなんて一体誰が決めたダスか(怒髪天衝)!!!
いずれにせよ生成文法派の存在感が凄すぎて語用論派の人々が彼らに対して超ナーバスになっているという流れがあってのことだと思います。そういえば英語教育で語用論派の先駆けとなった大先生の回想で、ヤング時代の学会発表時に学会長直々に(もちろん発表の不備に関してではなく語用論だという理由で)面罵されたというエピソードもありました。
昔の英語教育界は強面生成文法派が支配していて、割と語用論派が天下とった感じの今でもまだまだ残存して煮え煮えしているっぽい。てか、その人らが最近目立つところでも逆襲に出てますよね(笑?)。おーこわ。
ええと、なんかダラダラ書きましたが、まあ、頑張りまーすっ(←!)。
Copyright(c)2006-2015 ccoe@mac.com All rights reserved.