
母集団の母数θに関する尤度関数(likelihood function)は『すぐわかる統計用語』によれば、たとえば以下のように表せる。
L(θ) = L(x1,x2,...,xN;θ) = P(x1;θ)P(x2;θ)...P(xN;θ)
L(θ) = L(x1,x2,...,xN;θ) = f(x1;θ)f(x2;θ)...f(xN;θ)
母集団から取り出したN個のデータ(x1からxN)を確率変数X(random variable X)とする確率または確率密度の積である(...のだと思う)。
尤度比(likelihood ratio)は『すぐわかる統計用語』によれば「パラメータ空間の部分空間上での尤度関数の最大値」を分子とし、「パラメータ空間上での尤度関数の最大値」を分母とする値であるとされる。
独立性検定などでの場合を具体的に考えると帰無仮説が成り立つ部分空間と対立仮説が成り立つ部分空間とでパラメータ空間が形成されていると解釈できる。よって「帰無仮説が成り立つ部分空間上での尤度関数の最大値」を分子とし、「帰無仮説と対立仮説が成り立つ部分空間を含むパラメータ空間での尤度関数の最大値」を分母とする値として尤度比は求められることになる。(実際にやってみると分母は「対立仮説が成り立つ部分空間上での尤度関数の最大値」であるようにみえるが、帰無仮説が成り立つ際の最大値でもありえるので両方を含むパラメータ空間全体での最大値といえるのだろう)
| A | not A | ||
| B | c12 | c2-c12 | c2 |
| not B | c1-c12 | N-c1-c2+c12 | N-c2 |
| c1 | N-c1 | N |
上記のようなクロス集計表に関する尤度関数は次のようにして求められる。これらの比が尤度比である。
L1<-dbinom(c12,c1,c2/N)*dbinom(c2-c12,N-c1,c2/N)
L2<-dbinom(c12,c1,c12/c1)*dbinom(c2-c12,N-c1,(c2-c12)/(N-c1))
L1とL2はともに2項分布で求めた確率の積として計算され、L1が帰無仮説にあたる。dbinom(c12,c1,c2/N)は「AでありBである」場合の度数c12がc1という試行回数の中で出現する確率(母比率)をc2/N(度数総計NにおけるBの出現割合)と想定している。これは「AではないがBである」場合つまりdbinom(c2-c12,N-c1,c2/N)でも同じ値が使われる。
言い換えるとL1は「母比率c2/Nの事象」が「試行回数c1の中でc12回出現する確率」と「試行回数N-c1の中でc2-c12回出現する確率」との積を計算していることになる。「AでありBである(c1)」と「AではないがBである(c2-c12)」が想定母比率どおりの期待値のとき(それぞれの確率は最大値になるのでその積の)L1の値は最大値をとる。
これに対してL2では「AでありBである」ことの母比率をc12/c1、「AではないがBである」ことの母比率を(c2-c12)/(N-c1)と別々の想定をしている。これらは「Aである」列と「Aではない」列それぞれにおけるBの出現率をそのまま母比率と想定して計算された値なのでL2の値は常に最大値(実測値が期待値どおり)となる。
このことからL1/L2である尤度比は三種類の母比率(2項分布の母数=パラメータ)が合致するとき最大値の1になるということがわかる。反対に帰無仮説の母比率が、部分的な実測値をもとにした値(=対立仮説の母比率)と異なる度合いが大きいほどL1は小さい値になる。dbinom(c12,c1,c2/N)やdbinom(c2-c12,N-c1,c2/N)で求められるのは母比率がc2/Nである母集団(確率分布)に属していると仮定したときにc12やc2-c12という値をとる確率なので、期待値との相違が大きいほど有り得ない値とされて小さくなるからである。
尤度比とは帰無仮説が完璧に正しいとき最大値の1となり、帰無仮説が正しくない度合いが大きいほど0に近づく値なのだと確認できる。
ここまでのところで確認したように尤度比λは0から1までの範囲にある。λが1のときに対数をとれば0、これ以外の場合では分子が常に分母より小さい分数であることから対数をとるとマイナスになる。logλの範囲は0からマイナス無限大までと考えられるのである。これによって対数尤度比(loglikelihood ratio)は帰無仮説が完璧に正しいとき0となり、正しくない度合いが大きくなるほど負の方向に巨大化する値であるとわかる。
対数尤度比 logλを -2logλとすると帰無仮説が正しくない度合いに応じて0から正の方向で無限大までの範囲の数値となり、カイ2乗分布に近似する。
検定統計量に対数尤度比(logλ)を使う検定を対数尤度比検定(loglikelihood ratio test)という。検定統計量が -2logλ のときカイ2乗分布に従う。用途はカイ2乗検定と同じだが sparse data の分析に適している。ピアソンのカイ2乗検定(Chi-squared test)と区別してこちらはG検定(G-test)と呼ぶようである(→wikipedia"G-test")。
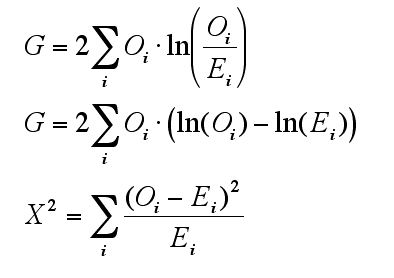
上記の式で計算するG値は -2logλすなわち -2log((likelihood for null model)/(likelihood for alternative model))と同じ値になる。
『マンガ統計手法入門』第12章のデータを使ってRで独立性の検定を行なう。これについては以前同じ対象に対する分析をカイ2乗検定に関して実行した(→参照)。
| シートベルト着用 | シートベルト未着用 | |
| 負傷した人 | 10533人 | 8896人 |
| 死亡した人 | 31人 | 167人 |
G2(matrix(c(10533, 8896, 31, 167), ncol=2, byrow=T))
#chisq.test(matrix(c(10533, 8896, 31, 167), ncol=2, byrow=T))
シートベルト着用の有無と被害の大きさに関係がない、とする帰無仮説を立てる。G2は「対数尤度比に基づく独立性の検定」で公開されているものを利用した。
G-squared = 125.8365, df = 1, p-value < 2.2e-16
#X-squared = 115.689, df = 1, p-value < 2.2e-16
自由度1のカイ2乗分布において検定統計量は(p-value < 0.05により)棄却域に入っているため、仮説は棄却できる。計算結果には若干の違いが見られるが結論は同じである。
『マンガ統計手法入門』第14章のデータを使ってRで検証する。これも以前カイ2乗検定で使ったデータである。
| チドリ | シギ | サギ | |
| 谷津干潟 | 210羽 | 2500羽 | 110羽 |
| 諫早干潟 | 350羽 | 3800羽 | 230羽 |
G2(matrix(c(210, 2500, 110, 350,3800,230), ncol=3, byrow=T))
#chisq.test(matrix(c(210, 2500, 110, 350,3800,230), ncol=3, byrow=T))
谷津干潟と諫早干潟で鳥の分布比に差がない、を帰無仮説として計算する。
G-squared = 8.1486, df = 2, p-value = 0.01700
#X-squared = 7.9816, df = 2, p-value = 0.01848
自由度2のカイ2乗分布において検定統計量は(p-value < 0.05により)棄却域に入っているため、仮説は棄却できる。統計量やp-valueの計算結果には若干の違いが見られるが結論には影響していない。
「フィッシャーの正確確率検定(Fisher's exact test)」で扱う標本数の少ないデータに対して対数尤度比検定を使った場合を比較する。
X <- matrix(c(13, 4, 6, 14), ncol=2, byrow=T)
G2(X)
#chisq.test(X)
#fisher.test(X, alternative="g")
分析結果は以下の通り。
G-squared = 8.2811, df = 1, p-value = 0.004006
#X-squared = 6.1922, df = 1, p-value = 0.01283
#p-value = 0.005855
ピアソンのカイ2乗検定よりはフィッシャーの正確確率検定に近い結果が出ている。
自然言語に関するデータで検定を行なった場合を比較する。『Foundations of Statistical Natural Language Processing』p.74の表から引用した。New York Times corpus の most powerfulというbigramについての値である。
X <- matrix(c(150, 12443, 782, 14294293), ncol=2, byrow=T)
G2(X)
#chisq.test(X)
#fisher.test(X, alternative="g")
分析結果は以下の通り。
G-squared = 1291.319, df = 1, p-value < 2.2e-16
#X-squared = 26973.53, df = 1, p-value < 2.2e-16
#p-value < 2.2e-16
帰無仮説の棄却については同じ結論となった。しかしG-squaredとX-squaredのふたつの検定統計量の食い違いはこれまでの例に比べて顕著に大きい。
>> 青木繁伸先生のサイト「対数尤度比に基づく独立性の検定」
>> 青木繁伸先生のサイト「フィッシャーの正確確率検定(直接確率)」