
確率変数X(random variable X)に対して確率密度関数f(x)が以下のようになるとき、これをカイ2乗分布(chi-square distribution)という。
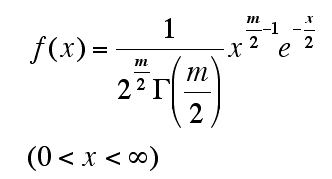
mは自由度(degrees of freedom)を表す。上式で使われているガンマ関数(gamma function)の数式は以下の通り。
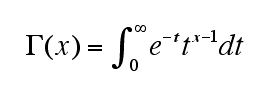
この関数は整数以外の階乗を計算するためのものらしく、t分布やF分布でも用いられる。
自由度3のときの確率密度分布と累積分布は以下のスクリプトで求められる。
dchisq(0:10,3)
pchisq(0:10,3)
グラフを描くスクリプトは次の通り。
ma<-2
mb<-4
mc<-8
md<-16
curve(dchisq(x,ma),0,30, type="l", lwd="2",col="purple",ylim=c(0,0.5))
#curve(pchisq(x,ma),0,30, type="l", lwd="2",col="purple",ylim=c(0,1))
par(new=TRUE)
curve(dchisq(x,mb),0,30, type="l",lwd="2", xlab="", ylab="", main="", axes=F,ylim=c(0,0.5),col="blue")
#curve(pchisq(x,mb),0,30, type="l",lwd="2", xlab="", ylab="", main="", axes=F,ylim=c(0,1),col="blue")
par(new=TRUE)
curve(dchisq(x,mc),0,30, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="orange",ylim=c(0,0.5))
#curve(pchisq(x,mc),0,30, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="orange",ylim=c(0,1))
par(new=TRUE)
curve(dchisq(x,md),0,30, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="red",ylim=c(0,0.5))
#curve(pchisq(x,md),0,30, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="red",ylim=c(0,1))
legend(9, 0.3, paste("m = ", c(2,4,8,16)), col=c("purple","blue","orange","red"), pch="ー", ncol=1)
#legend(20, 0.3, paste("m = ", c(2,4,8,16)), col=c("purple","blue","orange","red"), pch="ー", ncol=1)
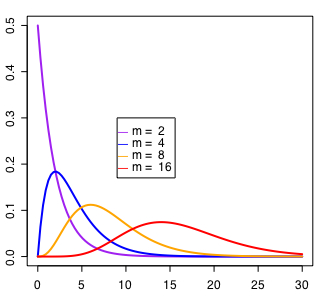
コメントアウトした(pchisqを使う)方で累積分布図が描ける。
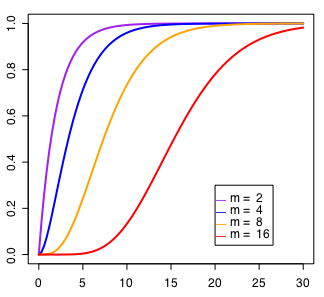
検定統計量がカイ2乗分布に従う検定をカイ2乗検定(chi-square test)という。「適合度検定(test of goodness of fit)」や「独立性の検定(test of independence)」などに用いる。
『マンガ統計手法入門』第13章のデータを使ってRで適合度検定を行なう。キイロショウジョウバエを数えて「野生型メス 592匹」「野生型オス 331匹」「白眼オス 281匹」だったとき、これが理論上の値「2:1:1」に適合しているのかそうでないのかを検定する。
chisq.test(c(592,331,281), p=c( 2, 1, 1)/4)
「観測値と理論値の間に差がない」という帰無仮説を立てて検定した結果は下記の通り。「Chi-squared test for given probabilities」が実行される。
X-squared = 4.485, df = 2, p-value = 0.1062
自由度2のカイ2乗分布において検定統計量は(p-value > 0.05により)棄却域に入っていないので仮説は棄却できない。よって「差があるのかないのかわからない」ということになる。p値(p-value)は「有意確率(observed significance level of the test)」ともいい、「有意水準(significance level)」と比較して小さい値であれば仮説を棄却する。
『マンガ統計手法入門』第12章のデータを使ってRで独立性の検定を行なう。
| シートベルト着用 | シートベルト未着用 | |
| 負傷した人 | 10533人 | 8896人 |
| 死亡した人 | 31人 | 167人 |
chisq.test(matrix(c(10533, 8896, 31, 167), ncol=2, byrow=T))
シートベルト着用の有無と被害の大きさに関係がない、とする帰無仮説を立てて「Pearson's Chi-squared test with Yates' continuity correction」を実行する。
X-squared = 115.689, df = 1, p-value < 2.2e-16
自由度1のカイ2乗分布において検定統計量は(p-value < 0.05により)棄却域に入っているため、仮説は棄却できる。つまりシートベルトの着用と交通事故被害に「独立性はない」=関連がある、ということがいえる。
「同等性の検証(test for equality)」は検定統計量が棄却域に入らなかったことを仮説成立と認めようという考えに基づいている。『マンガ統計手法入門』第14章のデータを使ってRで検証する。
| チドリ | シギ | サギ | |
| 谷津干潟 | 210羽 | 2500羽 | 110羽 |
| 諫早干潟 | 350羽 | 3800羽 | 230羽 |
chisq.test(matrix(c(210, 2500, 110, 350,3800,230), ncol=3, byrow=T))
谷津干潟と諫早干潟で鳥の分布比に差がない、という仮説を立てる。「Pearson's Chi-squared test」が実行される。
X-squared = 7.9816, df = 2, p-value = 0.01848
自由度2のカイ2乗分布において検定統計量は(p-value < 0.05により)棄却域に入っているため、仮説は棄却できる。つまりふたつの干潟で鳥の分布比に差がある、ということがいえる。
pwr.chisq.test(w=0.01848, N=6,df=2,sig.level=0.05)
この例では仮説が棄却されてしまっているので扱わなかったが、通常「同等性の検証」では「検出力(power of test)」の値をみて「同等かどうか」を判断する。上のスクリプトによって power = 0.0501535 が算出できる。power > 0.8 のとき「仮説が成り立つ」と判断する。
「フィッシャーの正確確率検定(Fisher's exact test)」では超幾何分布を利用して p-value を求める。標本数が極僅かであるなど、カイ2乗検定で扱いにくいデータに対して使用する。用途はカイ2乗検定と同様「独立性の検定」や「母集団の母比率比較」などである。
与えられたデータに対して超幾何分布を用いて確率を計算する。与えられた行列に対して分子は「各行(row)の総和の階乗と各列(column)の総和の階乗の積」で、分母は「値の総和の階乗と各値の階乗の積」である。
まず観察されたデータに対してこれを行なうことで生起確率を得る。
次に各行の総和と各列の総和を固定したままで、各値を変化させることで得られる状態すべてについて生起確率を計算する。2×2行列(1行目a,b 2行目c,d)の場合、独立性を検定する要因同士の関連の強さをみるために ad-bc を計算し、観測されたデータよりもその値が大きいものの生起確率の総和と観測されたデータの生起確率の和を求める(片側検定の場合)。こうして求めた値が p-value < 0.05 のとき帰無仮説は棄却される。
次の2×2クロス集計表を観測されたデータとして計算する。
| B1 | B2 | |
| A1 | 1 | 2 |
| A2 | 3 | 4 |
X <- matrix(c(1, 2, 3, 4), ncol=2, byrow=T)
#chisq.test(X)
fisher.test(X, alternative="g")
カイ2乗検定の結果には「Warning message:カイ自乗近似は不正確かもしれません」というアラートが出た。それでも一応「X-squared = 0.1786, df = 1, p-value = 0.6726」が算出される。「Fisher's Exact Test for Count Data」では p-value = 0.8333 となる。フィッシャーの正確確率検定を手作業で計算してみる。上記のクロス集計表の場合、次の4つの場合が存在する。
a=0,b=3,c=4,d=3(ad-bc=-12, P0=0.1666667)
a=1,b=2,c=3,d=4(ad-bc=-2, P1=0.5)
a=2,b=1,c=2,d=5(ad-bc=8, P2=0.3)
a=3,b=0,c=1,d=6(ad-bc=17, P3=0.03333333)
観測されたデータP1を含んでそれより ad-bc が大きいのはP2,P3なのでその総和である p-value は 0.5+0.3+0.33333...=0.833333...となり、fisher.test の計算結果と一致する。
>> EMANの物理学「ガンマ関数」
>> R-Tips 66節「カテゴリカルデータの検定」
>> 奥村晴彦先生のサイト「カイ2乗検定」
>> 青木繁伸先生のサイト「フィッシャーの正確確率検定(直接確率)」