
データ X と Y(データ個数が N)に関するピアソンの相関係数(Peason's correlation coefficient)は以下の数式で表せる。
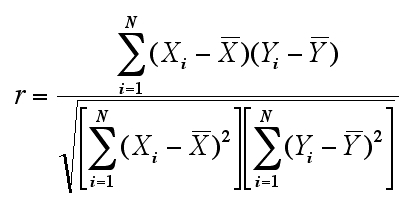
相関係数の分子は X と Y の共分散(covariance)で分母は X の分散の平方根と Y の分散の平方根の積である。しかし N-1 は約分されるので、分子は積和(cross product)で分母は平方和(sum of squares)の平方根の積という形になる。
N行(rows)×2列(columns)で行名(1,2,3...N)と列名(X、Y)がついたcsv形式の表を作成していた場合、以下のように読み込む。
test<-read.csv("data.csv", header=T)
test_frame<-data.frame(test, row.names=T)
#colnames(test_frame)<-c("X","Y")
列名はこの例のように X や Y 程度であればそのまま通るが日本語などの場合は勝手に置き換えられてしまう。コメントアウトした行のように colnames を使って指定しなくてはならない。このとき相関係数は次のスクリプトで計算できる。
cor(test_frame$X, test_frame$Y)
#cor(test_frame$X, test_frame$Y, method="spearman")
#cor.test(test_frame$X, test_frame$Y, method="pearson")
#(cor(test_frame$X, test_frame$Y))^2
コメントアウトした行のひとつめはデータが順位の場合に使う「スピアマンの順位相関係数ρ」を手法として選択している。ふたつめは無相関かどうかの検定を行なうスクリプトである。methodは省略するとピアソンのものが指定されるようだ。みっつめは回帰分析などの当てはまり具合を調べる際に使う決定係数(coefficient of determination)を求めている。
重回帰分析(multiple regression analysis)は目的変量の値を説明変量の値に基づいて予測するのに使う。単回帰分析(simple regression analysis)を一般化したものである。
『マンガ統計手法入門』第8章のデータを使ってRで重回帰分析を行なう。「エビの消費量」と「飲食店数」というふたつの説明変量と、目的変量である「エビの生産量」との関係についての重回帰式を求める。
ebi<-read.csv("ebi.csv", header=T)
ebi_frame<-data.frame(ebi, row.names=T)
colnames(ebi_frame)<-c("production","rester","consumption")
ebi_lm<-lm(production~., data=ebi_frame)
ebi_frame において列名 production を目的変量とした重回帰分析を行ない、その結果を ebi_lm に格納している。ただし、ebi_lm と入力するだけでは以下のものしか表示されない。
Call:
lm(formula = production ~ ., data = ebi_frame)
Coefficients:
(Intercept) rester consumption
-2.35396 0.18051 0.01493
これは偏回帰係数( partial regression coefficient)と定数であるので、重回帰式を求めるだけなら一応事足りてしまう。重回帰式は「生産量 = -2.35596 + 0.18051*店舗数 + 0.01493*消費量」になる。詳しい分析結果や当てはまり具合については summary(ebi_lm) を使う。
Call:
lm(formula = production ~ ., data = ebi_frame)
Residuals:
1965 1970 1975 1980 1985
0.1118 -0.1663 0.5612 -1.9372 1.4305
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.353959 2.770326 -0.850 0.485
rester 0.180505 0.090523 1.994 0.184
consumption 0.014929 0.009229 1.618 0.247
Residual standard error: 1.754 on 2 degrees of freedom
Multiple R-Squared: 0.9607, Adjusted R-squared: 0.9214
F-statistic: 24.45 on 2 and 2 DF, p-value: 0.03929
「Residuals:」は残差のことで、これは実測値から予測値を引いた値である。相対的には1975はやや大きく、1980と1985はかなり大きいとわかる。残差が大きいということは当てはまりが悪いということである。
次の「Coefficients:」においては、各説明変量が予測に役立つかどうかの検定なども行なっている。「この説明変量は予測の役に立たない」という帰無仮説を立ててt検定をした結果「Pr(>|t|)」が 0.05 より大きければ仮説が棄却されないので「予測に役立つ」とはされない。上の例ではすべての説明変量が「なくてもよい」レベルであることが示唆されている。(←この件についてはよく理解できていないため間違いを書いているかもしれません、ごめんなさい)
その他、t値の左側の値は標準誤差(「Std. Error」)といって偏回帰係数をこれで割った値がここでのt値である。標準誤差は偏回帰係数の標準偏差のことなので値が小さいほど当てはまりが良いことになる。
下から2行目の「Multiple R-Squared」は「重相関係数 R を2乗した値」=「決定係数」である。重相関係数は実測値と予測値の間の相関係数を指す。この値が 1 に近いほど予測値の当てはまりが良いことになる。また「Adjustered R-squared」は自由度調整済決定係数のことで、説明変量の個数が増えるにつれて決定係数が大きくなる不具合を調整したものであり、この値は常に決定係数以下となる。
最終行ではF検定を行なっている。帰無仮説は「この重回帰式は予測の役に立たない」というもので、p-value < 0.05 なので仮説は棄却される。(←このF値がどこから出て来たのか理解できていません、すみません)
この他、ebi_lm2<-step(ebi_lm) を使うと次のような結果となる。
Start: AIC= 7.04
production ~ rester + consumption
Df Sum of Sq RSS AIC
<none> 6.1541 7.0384
- consumption 1 8.0516 14.2057 9.2210
- rester 1 12.2347 18.3888 10.5115
AICは「赤池情報量規準」で当てはまりの良さを評価する値である。(←stepに関する項目についてもよく理解できていません、ごめんなさい)
作図によって妥当性をチェックする。Rスクリプトと作図結果は以下の通り。
plot.lm(ebi_lm,which=1)
abline(h=0)
#plot.lm(ebi_lm,which=2)
#
#plot(resid(ebi_lm))
#qqnorm(resid(ebi_lm))
#qqline(resid(ebi_lm))
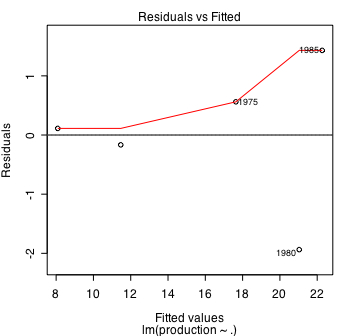
plot.lm を使う場合と使わない場合に分けられる。plot.lm を使ってwhich=1 だと「残差プロット」を描く。 which=2 の場合は「Q-Qプロット」になる。両図とも回帰直線から外れる度合いの高いものについてだけ行名を表記しているようだ。
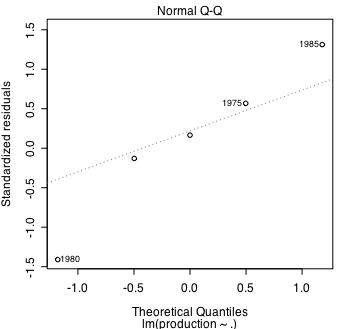
plot.lm を使わないでQ-Qプロットを描いた結果は次のようになる。
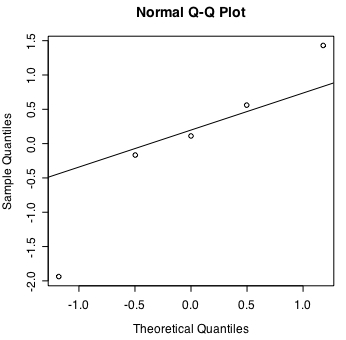
ちなみに resid(ebi_lm) の結果は行名を列名にして残差データだけを残す。
1965 1970 1975 1980 1985
0.1117628 -0.1662932 0.5612081 -1.9371774 1.4304997
特にラベルが必要なければ残差の数値データだけを対象としてQ-Qプロットが描ける。
この他様々な方法があるが説明は割愛する。
>> R-Tips 67節「相関係数と無相関検定」
>> R-Tips 71節「回帰分析と重回帰分析」