分布と検定　その３

t分布

■ 数式

確率変数X（random variable X）に対して確率密度関数f(x)が以下のようになるとき、これをt分布（t distribution）という。

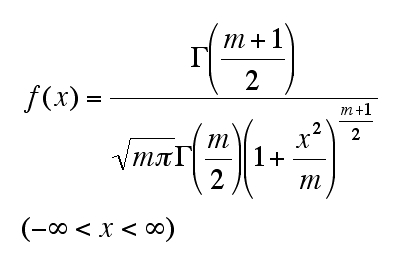
mは自由度（degrees of freedom）を表す。

■ Rスクリプト

自由度10のときの確率密度分布と累積分布の基本的グラフは以下のスクリプトで求められる。

curve(dt(x,10),-5,5)
curve(pt(x,10),-5,5)

自由度を変えてグラフを描くスクリプトは次の通り。

ma<-2
mb<-4
mc<-16
md<-256
curve(dt(x,ma),-5,5, type="l", lwd="2",col="purple",ylim=c(0,0.5))
#curve(pt(x,ma),-5,5, type="l", lwd="2",col="purple",ylim=c(0,1))
par(new=TRUE)
curve(dt(x,mb),-5,5,, type="l",lwd="2", xlab="", ylab="", main="", axes=F,ylim=c(0,0.5),col="blue")
#curve(pt(x,mb),-5,5, type="l",lwd="2", xlab="", ylab="", main="", axes=F,ylim=c(0,1),col="blue")
par(new=TRUE)
curve(dt(x,mc),-5,5, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="orange",ylim=c(0,0.5))
#curve(pt(x,mc),-5,5, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="orange",ylim=c(0,1))
par(new=TRUE)
curve(dt(x,md),-5,5, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="red",ylim=c(0,0.5))
#curve(pt(x,md),-5,5, type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="red",ylim=c(0,1))
legend(2, 0.3, paste("m = ", c(2,4,16,256)), col=c("purple","blue","orange","red"), pch="ー", ncol=1)
#legend(2, 0.5, paste("m = ", c(2,4,16,256)), col=c("purple","blue","orange","red"), pch="ー", ncol=1)

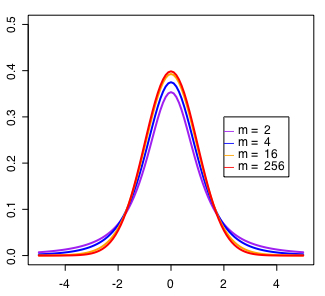
コメントアウトした（ptを使う）方で累積分布図が描ける。

t検定

■ 用途

検定統計量がt分布に従う検定をt検定（t test）という。「母平均の検定」や「ふたつの母平均の差の検定」などに用いる。

■ ふたつの母平均の差の検定

『マンガ統計手法入門』第2章のデータを使ってRでt検定を行なう。ウェイトレスとコンパニオンの時給の母平均に差があるのかどうかを検定する。

Data1<-c(850,1000,1100,950,1200,900,1050,800)
Data2<-c(1400,1500,2200,2000,2500,2300,1600)
t.test(Data1,Data2)
#t.test(Data1,Data2,var.equal=TRUE)

コメントアウトした方は母分散に差がないと想定した場合の検定で、何も設定しないと Welch の検定になる。結果は以下の通り。

t = -5.5863, df = 7.007, p-value = 0.0008249

p-value が 0.05 より小さいので「差がない」という帰無仮説は棄却される。作図するRスクリプトは以下の通り。

#自由度
m<-7.007
#検定統計量と生起確率
xt<--5.5863
yt<-dt(xt,m)
#棄却域
xz<-qt(0.975,m)
yz<-dt(xz,m)
#t分布曲線
curve(dt(x,m),-6,6,ylim=c(0,0.4),xlim=c(-6,6))
par(new=TRUE)
#検定統計量のプロット
plot(xt,yt,ylim=c(0,0.4),xlim=c(-6,6),xlab="", ylab="", main="", axes=F,col="black")
par(new=TRUE)
#棄却域のプロット
xzm<-c(xz,-xz)
yzm<-c(yz,yz)
plot(xzm,yzm,ylim=c(0,0.4),xlim=c(-6,6),xlab="", ylab="", main="", axes=F,col="red")
par(new=TRUE)
#補助線
segments(xz,0,xz,yz,lty=1,col="red")
segments(xz,0,6,0,lty=1,col="red")
segments(-xz,0,-xz,yz,lty=1,col="red")
segments(-xz,0,-6,0,lty=1,col="red")
segments(-xz,0,xz,0,lty=1,col="blue")
#説明
legend(2, 0.3, paste("m = 7.007"))

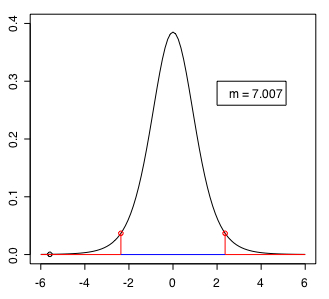
この場合の検定統計量を示す黒い点（-5.5863,0.0004326513）は信頼区間（confidence interval）を大きく外れている。自由度7.007のときの信頼限界（confidence limit）を示す赤い点は（2.364145,0.0367915）及びその正負逆の値となる。

F分布

■ 数式

確率変数X（random variable X）に対して確率密度関数f(x)が以下のようになるとき、これをF分布（F distribution）という。

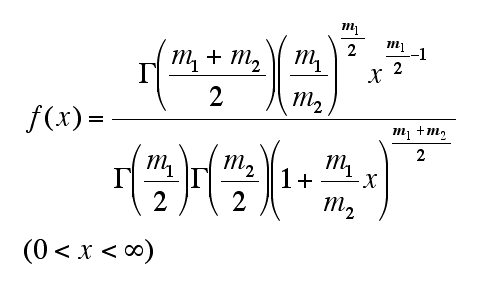
F分布では自由度がふたつ（m1とm2）必要になる。

■ Rスクリプト

自由度4と5のときの確率密度分布と累積分布の基本的グラフは以下のスクリプトで求められる。

curve(df(x,4,5),0,10)
curve(pf(x,4,5),0,10)

自由度を変えてグラフを描くスクリプトは次の通り。

ma<-2
ma2<-4
mb<-2
mb2<-16
mc<-4
mc2<-2
md<-16
md2<-2
curve(df(x,ma,ma2),0,6, type="l", lwd="2",col="purple",ylim=c(0,1.0))
#curve(pf(x,ma,ma2),0,10, type="l", lwd="2",col="purple",ylim=c(0,1.0))
par(new=TRUE)
curve(df(x,mb,mb2),0,6, type="l",lwd="2", xlab="", ylab="", main="", axes=F,ylim=c(0,1.0),col="blue")
#curve(pf(x,mb,mb2),0,10, type="l",lwd="2", xlab="", ylab="", main="", axes=F,ylim=c(0,1.0),col="blue")
par(new=TRUE)
curve(df(x,mc,mc2),0,6,type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="orange",ylim=c(0,1.0))
#curve(pf(x,mc,mc2),0,10,type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="orange",ylim=c(0,1.0))
par(new=TRUE)
curve(df(x,md,md2),0,6,type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="red",ylim=c(0,1.0))
#curve(pf(x,md,md2),0,10,type="l",lwd="2", xlab="", ylab="", main="", axes=F,col="red",ylim=c(0,1.0))
legend(2, 0.6, paste("(m1,m2) = ", c("(2,4)","(2,16)","(4,2)","(16,2)")), col=c("purple","blue","orange","red"), pch="ー", ncol=1)
#legend(5, 0.5, paste("(m1,m2) = ", c("(2,4)","(2,16)","(4,2)","(16,2)")), col=c("purple","blue","orange","red"), pch="ー", ncol=1)

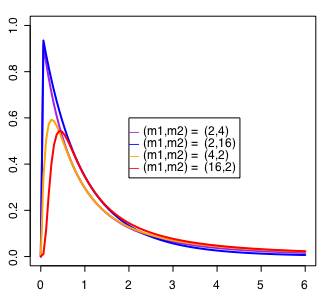
コメントアウトした（pfを使う）方で累積分布図が描ける。

F検定

■用途

検定統計量がF分布に従う検定をF検定（F test）という。「ふたつの母分散の差の検定」などに用いる。

■ふたつの母分散の差の検定

『マンガ統計手法入門』第2章のデータを使ってRでF検定を行なう。ウェイトレスとコンパニオンの時給の母分散に差があるのかどうかを検定する。

Data1<-c(850,1000,1100,950,1200,900,1050,800)
Data2<-c(1400,1500,2200,2000,2500,2300,1600)
var.test(Data1,Data2)

結果は以下の通り。

F = 0.0959, num df = 7, denom df = 6, p-value = 0.006802

p-value = 0.006802 は 0.05 よりも小さいので「母分散に差はない」という帰無仮説は棄却される。作図するRスクリプトは以下の通り。

#自由度
m1<-7
m2<-6
#検定統計量と生起確率
xf<-0.0959
yf<-df(xf,m1,m2)
#棄却域
xz<-qf(0.975,m1,m2)
yz<-df(xz,m1,m2)
xl<-qf(0.025,m1,m2)
yl<-df(xl,m1,m2)
#F分布曲線
curve(df(x,m1,m2),0,10,ylim=c(0,0.7),xlim=c(0,10))
par(new=TRUE)
#検定統計量のプロット
plot(xf,yf,ylim=c(0,0.7),xlim=c(0,10),xlab="", ylab="", main="", axes=F,col="black")
par(new=TRUE)
#棄却域のプロット
plot(xz,yz,ylim=c(0,0.7),xlim=c(0,10),xlab="", ylab="", main="", axes=F,col="red")
par(new=TRUE)
#棄却域のプロット2
plot(xl,yl,ylim=c(0,0.7),xlim=c(0,10),xlab="", ylab="", main="", axes=F,col="red")
par(new=TRUE)
#補助線
segments(xz,0,xz,yz,lty=1,col="red")
segments(xz,0,10,0,lty=1,col="red")
segments(xl,0,xl,yl,lty=1,col="red")
segments(xl,0,0,0,lty=1,col="red")
segments(xl,0,xz,0,lty=1,col="blue")
#説明
legend(4, 0.4, paste("(m1,m2) = (7,6)"))

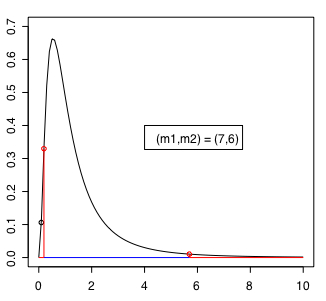
この場合の検定統計量を示す黒い点（0.0959,0.1061912）は棄却域に入っている。自由度（7,6）のときの信頼限界を示す赤い点は（5.69547,0.01042083）及び（0.1953660,0.3299347）である。

参考にしたサイトなど

>> R-Tips 65節「二標本検定」
>> 奥村晴彦先生のサイト「t検定」

▼研究関連メモ目次へ戻る