
確率変数X(random variable X)の値が0を含む任意の自然数x(ただし n 以下 )のとき、確率分布は次の数式によって表される。(参考)
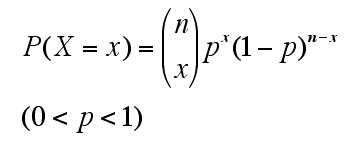
これは2項分布(binomial distribution)またはベルヌイ分布(Bernoulli distribution)と呼ばれ B(n,p) と書く。n は標本の規模、p はこの事象が起る確率のことである。
コインを投げて表が出る確率 p が 0.5 で100回試行した場合(n=100)の2項分布は B(100,0.5) と書ける。このとき、表がちょうど44回出る確率 P(X=x=44) を求めるスクリプトは以下の通り。
dbinom(44,100,0.5)
「0.03895256」が算出される。次に確率分布図を plot を使った方法と curve を使った方法の二種類のやり方で描く。まずは plot を使ったもの。
plot(dbinom(0:100,100,0.5),type="h",lwd="2")
par(new=TRUE)
plot(dbinom(0:100,100,0.5),type="l",lwd="1", xlab="", ylab="", main="", axes=F)
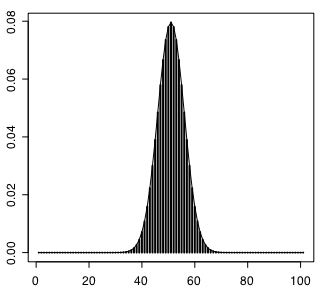
最初の plot でヒストグラムを作図している(type="h")。lwdは線の太さの指定に使う。ふたつめの plot で線を重ねて表示した(type="l")。
np=100*0.5=50 つまり平均値(mean)周辺だけが高い確率となっているので、グラフに表示する範囲を狭めたい。その場合は以下のように指定する。
plot(dbinom(0:100,100,0.5),type="h",lwd="2",xlim=c(30,70))
#plot(dbinom(30:70,100,0.5),type="l",lwd="2")
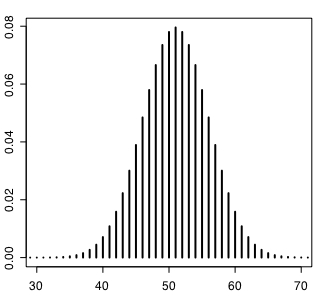
x軸の度数が 50 ではなく 51 のところに確率のピークがきているが、これは作図が度数0ではなく1から始まっているためである。つまり dbinom(0,100,0.5) が度数1なのである。しかし dbinom(50,100,0.5) の結果が 0.07958924 であり dbinom(49,100,0.5)と dbinom(51,100,0.5)はともに 0.07802866 となるので、こちらの計算ではズレているわけではない。
curve(dbinom(x,100,0.5),0,100,101,xlim=c(30,70))
#curve(dbinom(x,1000,0.5),0,1000,1001,xlim=c(440,560))
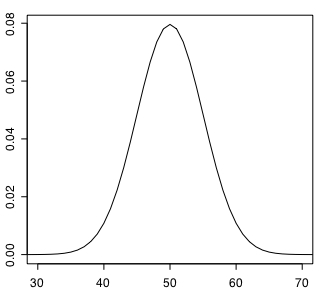
curve を使った作図法についてはよくわからない部分がある。
確率変数Xの値が0を含む任意の自然数xのとき、予め平均λ回起きるとわかっている事象の確率分布は以下のように表せる。
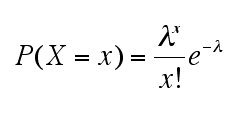
これはポアソン分布(Poisson distribution)と呼ばれ、希にしか起らない事象について当てはまるといわれている。
「透明中隔嚢胞(透明中隔腔)」が大人になっても残っている人間は100人にひとり程度と言われ、頭部の損傷等で検査を受けた折りに偶然発見される。今、酒場にいる客200人をつかまえて手当り次第にMRIに放り込んだ場合、ちょうど3人の脳にこれが発見される確率 P(X=x=3) はどうなるか。
prob<-1/100約「0.18」が算出される。plot を使ったRスクリプトと作図例は以下の通り。
size<-200
lambda<-prob*size
round(dpois(3,lambda),3)
prob<-1/100
lambdaa<-prob*100
lambdab<-prob*500
lambdac<-prob*1000
lambdad<-prob*1500
plot(dpois(0:30,lambdaa), type="l", lwd="1",col="green",ylim=c(0,0.4))
par(new=TRUE)
plot(dpois(0:30,lambdab), type="l",lwd="1", xlab="", ylab="", main="", axes=F,ylim=c(0,0.4))
par(new=TRUE)
plot(dpois(0:30,lambdac), type="l",lwd="1", xlab="", ylab="", main="", axes=F,col="blue",ylim=c(0,0.4))
par(new=TRUE)
plot(dpois(0:30,lambdad), type="l",lwd="1", xlab="", ylab="", main="", axes=F,col="red",ylim=c(0,0.4))
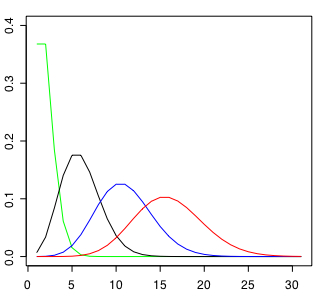
λが 1,5,10,15 の4つのケースについて作図した。
確率変数Xに対して F(x)=P(X<x) を累積分布関数(cummulative distribution function)といい、これが微分可能なとき、導関数 f(x) を確率密度関数(probability density function)と呼ぶ。
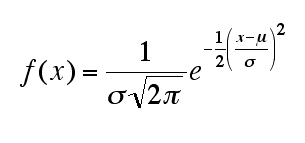
上記の式で与えられる確率分布が正規分布(normal distribution)である。μは平均値、σは標準偏差(つまりσの二乗は分散)を意味し、 N(μ,σ^2)と書く。確率そのものは定積分で得られる。
2項分布やポアソン分布は離散型確率分布(discrete distribution)であるが、正規分布は連続型確率分布(continuous distribution)なので確率分布の性質が異なる。
正規分布 N(np,np(1-p)) において平均値と分散がそれぞれ十分に大きいとき、2項分布 B(n,p) と近似するといわれる。B(100,0.5)と N(50,25) を比較して確認する。
plot(dbinom(0:100,100,0.5),type="h",lwd="3",col="gray",xlim=c(30,70))
par(new=TRUE)
plot(dnorm(0:100,mean=50,sd=5),type="l",lwd="1", xlab="", ylab="", main="", axes=F,xlim=c(30,70),col="orange")
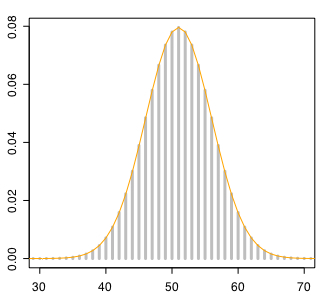
どちらも直線で描くと完全に一致してしまうのため2項分布はヒストグラムで描いた。
正規分布 N(λ,λ)はλが十分大きいとき、ポアソン分布と近似するとされる。λ=15のポアソン分布とN(15,15)を比較して確認する。
plot(dpois(0:30,15), type="l", lwd="1",col="blue")
par(new=TRUE)
plot(dnorm(0:30,mean=15,sd=sqrt(15)),type="l",lwd="1", xlab="", ylab="", main="", axes=F,col="red")
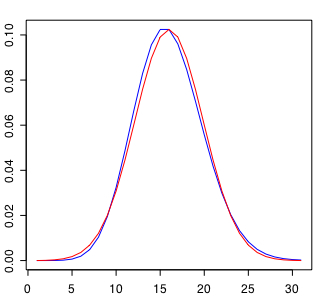
λ=15ではまだ十分大きいとはいえないようで、ズレがみられる。
2項分布 B(n,λ/n)において n が巨大な値をとるとき、ポアソン分布と近似するとされる。n=100000 、λ=15 として両分布を比較する。
plot(dpois(0:30,15), type="h", lwd="3",col="gray")
par(new=TRUE)
plot(dbinom(0:30,100000,15/100000),type="l",lwd="1", xlab="", ylab="", main="", axes=F,col="orange")
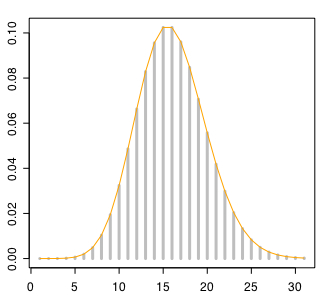
直線で描いて重ねると完全に一致してしまうので2項分布はヒストグラムで表した。
>> R-Tips 第60節「確率分布と乱数」
>> バイオインフォマティクスって何ですか?「Rでポアソン分布」
>> 奥村晴彦先生のサイト「ポアソン分布」